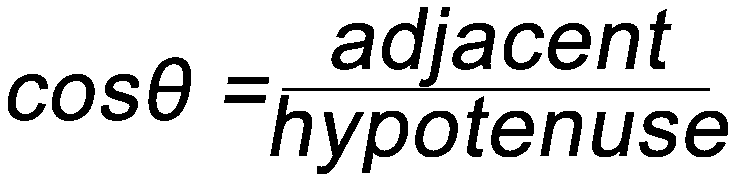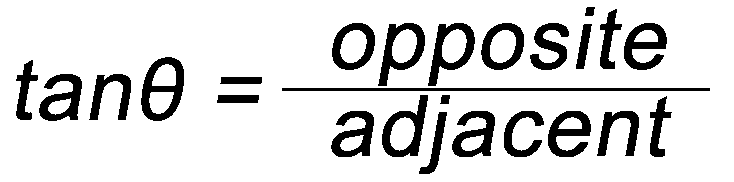-
The Metric System (MKS system) has seven fundamental units. They are
- M eter : distance
- K ilogram : mass (roughly “how many atoms make up an object”)
- S econd : time
- Ampere: electric current (how many atoms are flowing)
- Mole : the number of atoms needed to equal the atomic mass number in grams (1 mole of Carbon has a mass of 12 g and contains 6.022…×10 23 atoms)
- Kelvin : temperature
- Candela : light
-
Prefixes are also used to increase or decrease the size of any unit.
- Some Common Prefixes
- Tera- T 1012 “trillion” (Terabyte computer hard drive)
- Giga- G 109 “billion” (1.21 Gigawatts of energy to power the flux capacitor)
- Mega- M 106 “million” (Mega! Big! M! Million!)
- Kilo- K 103 “thousand” (a kilometer is like a metric mile, 1,000 meters like 1,000yards)
- centi- c 10-2 “one hundredth” (100 cents in a dollar ∴ one cent is 1/100th of a dollar)
- milli- m 10-3 “one thousandth” (a millipede has, like, a thousand legs)
- micro- µ (mu) 10-6 “one millionth” (million and micro both start with “m”)
- nano- n 10-9 “one billionth” (nono- nino- nine zeroes)
-
All physical measurements are subject to error. Errors may stem from the method used, environmental fluctuations, instrument limitations, or personal error.
-
Systematic errors are in one direction only.
-
Random errors are in both directions and may be reduced by large numbers of observations (repeated trials).
-
Tolerance is the amount of accepted error. It leads to a Range of acceptable values.
-
The accuracy of a measurement refers to how closely it agrees with an accepted value. (AKA percent deviation or percent error)
-
Precision is the degree of exactness of a measurement and is determined by the instrument used.
- For handheld instruments the precision is half the smallest mark (which is estimated).
-
Significant figures are those known to be reasonably reliable. Therefore all measured figures and one estimated figure would be considered significant.
- Digits 1 to 9 are always significant. Zeroes are significant when they appear between digits; if they follow digits a decimal must be present in the number for the zeroes to be significant.
- Addition and Subtraction: When adding or subtracting numbers, your answer will have the same number of significant figures after the decimal as the least precise number used.
- For example: 25.678 + 3.45 + 67.2 = 96.3
- Only to the tenths place
- Multiplication and Division: When multiplying or dividing numbers, your answer cannot have more total significant figures than the smallest total number of significant figures in any of the numbers used to obtain the answer.
- For example: (26.4 N)(1.2 m) = 32 N•m Only two significant figures
- These rules are fairly easy to follow until you begin introducing zeros into your equations. Below are some examples using zeros.
- 700 has only one significant figure (the 7).
- 700.0 has 4 significant figures (all 4 numbers).
- 0.0700 has 3 significant figures (the 7 and the two zeros to the right of the 7).
- 0.007 has only 1 significant figure (the number 7).
- 7.007 has 4 significant figures (all 4 numbers).
-
For very large and very small quantities we write numbers in scientific notation.
Greek Alphabet- used as variables or symbols Many letters represent specific values or measurements
| Use in Physics |
Capital |
Name |
Lower Case |
Use in Physics |
| |
Α |
Alpha |
α |
angle |
| |
Β |
Beta |
β |
angle |
| torque |
Γ |
Gamma |
γ |
E/mc2, angle |
| change |
Δ |
Delta |
δ |
small change |
| |
Ε |
Epsilon |
ε |
electromotive force |
| |
Ζ |
Zeta |
ζ |
|
| |
Η |
Eta |
η |
index of refraction |
| angle |
Θ |
Theta |
θ |
most common symbol for angle |
| |
Ι |
Iota |
ι |
rarely used- looks too much like i |
| |
Κ |
Kappa |
κ |
|
| rate, lambda baryon |
Λ |
Lambda |
λ |
wavelength, rate |
| |
Μ |
Mu |
μ |
coefficient of friction, muon, micro- |
| |
Ν |
Nu |
ν |
frequency, nutrino |
| charmed baryon |
Ξ |
Xi |
ξ |
|
| |
Ο |
Omicron |
ο |
rarely used- looks like 0 |
| product operator |
Π |
Pi |
π |
Hello! Pi! also a pion |
| |
Ρ |
Rho |
ρ |
density, resistivity |
| sum of |
Σ |
Sigma |
σ |
conductivity, cross section, area density |
| |
Τ |
Tau |
τ |
mean lifetime, tau lepton |
| |
Υ |
Upsilon |
υ |
rearely used- look slike v |
| wave function, angle |
Φ |
Phi |
φ |
wave function, angle |
| |
Χ |
Chi |
χ |
|
| wave function |
Ψ |
Psi |
ψ |
wave function |
| |
Ω |
Omega
|
ω |
angular frequency |
Unit Conversions
-
Before you solve an exercise, it is important that all units on the ends of the numbers you are using be in the same system. Most of the quantities you will see this year use the SI System (Systeme International), which is the standard system of units in physics.
-
To convert units into an equivalent amount using different units you will need to multiply by fractions which equal 1 and cancel out like units.
- For example: To convert 5 years into seconds.
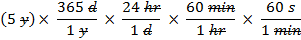
-
Notice that anything you are trying to eliminate in the numerator must be written in the denominator and vice versa.
-
The units appearing in both the numerator and denominator cancel each other out, as shown by the slash marks through them.
-
Multiplying the numerators gives: 5 x 365 x 24 x 60 x 60= 157,680,000
-
Multiplying the denominators gives: 1 x 1 x 1 x 1=1
-
Final answer: 157,680,000s/1 = 157,680,000 s. Note: This number is not written with significant figures.
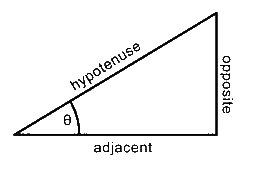
Dimensional Analysis Some Simple Trigonometry Relationships
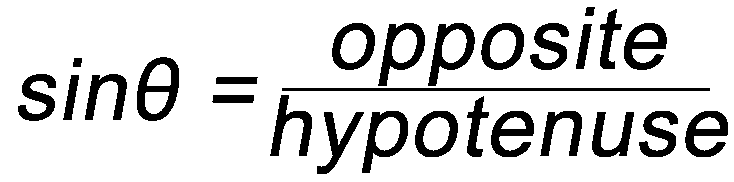
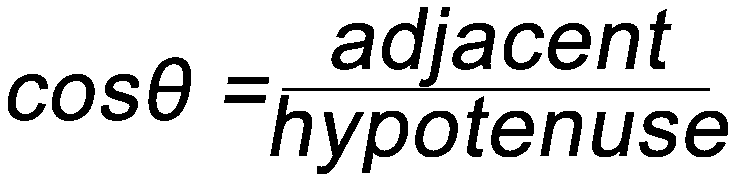
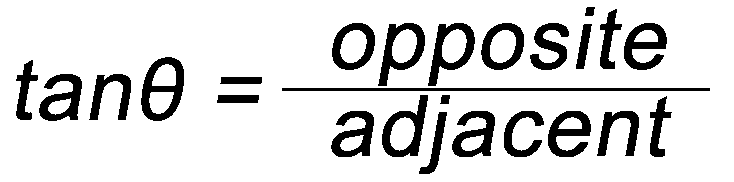
- Remember, you can only use the above relationships with right triangles. The hypotenuse of a right triangle is always the longest side.
|