Horizontal Projectiles

Consider this:

A ball rolling across a frictionless surface, with no air resistance, at 2m/s will continue rolling at 2 m/s forever.

In space, with no air resistance and no surface to rest on, the ball will go in a
straight line at the same speed forever.

Now plot this on a graph:

Set up a graph in portrait orientation (up & down “hot dog”). Place the x-axis at
the top and number it 0 through 70 as shown below. The label the y-axis 0 - 175
(every 25 works nicely) with the zero at the top.

Speed Links
These will take you to sections below.

• Horizontally Launched Projectiles 1
• Horizontally Launched Projectiles 2
• Horizontally Launched Projectiles 3
• Free body diagrams worksheet
• Life on an Elevator worksheet

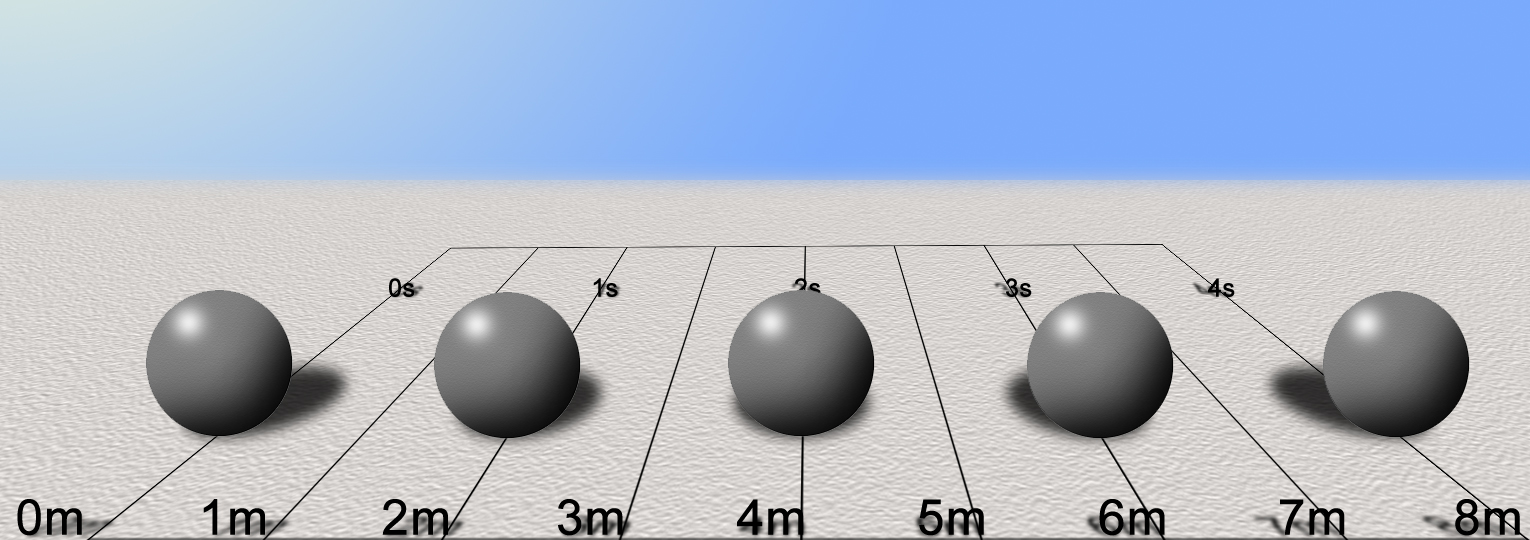
Now add the velocity vectors (10m/s for each). The arrows should be 10m long.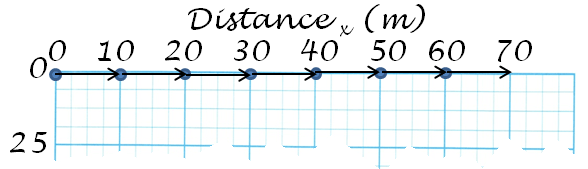

A dropped ball will fall straight down with an acceleration of 9.81m/s².
Using d = ½at², calculate the total distance the ball has traveled from its
release point for each of the following:

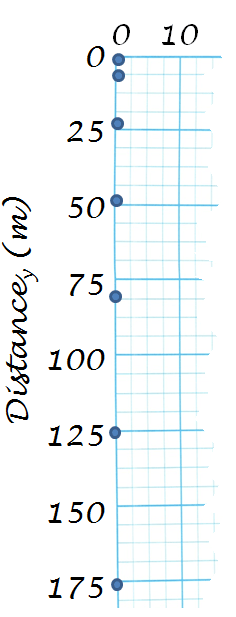
Now plot this on the graph:

Calculate the velocity of the fall:v = at

Now draw in the velocity vectors using the velocities calculated in the table above.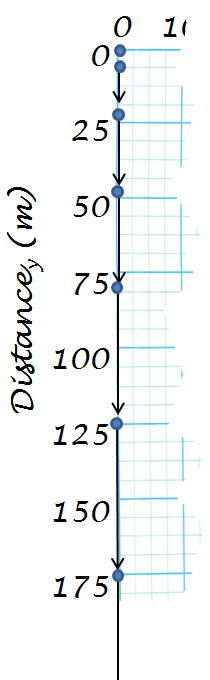

Note: the bottom vector goes off the chart which is ok. You get the idea.

Finally, put it all together. Plot the x- and y-coordinates and add the
vertical and horizontal vectors all together.

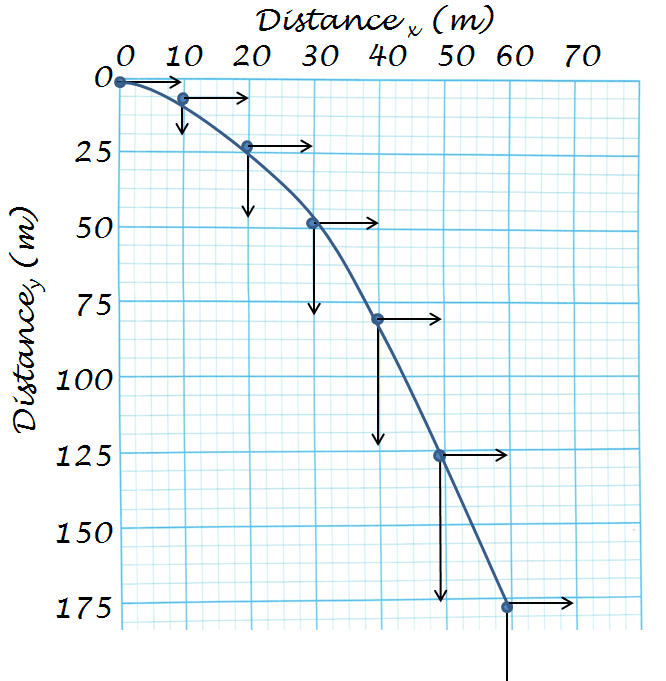
With a horizontally launched projectile, it has the properties of a horizontally
moving object with constant speed, while behaving like a dropped object
accelerating with the pull of gravity. When the projectile is graphed it takes
on a curved, parabolic arc, showing the accelerated downward movement
while maintaining its constant horizontal speed.

As such, when solving horizontal projectile problems, it is usually helpful to
divide these two behaviors from each other. Solve all problems as a vertical
free-fall problem, then as a horizontal constant motion problem.

To sum up Horizontal Projectile Motion:

A virtual demonstration:
TwoBallsGravity.html

Practice Problem:

A plane flying horizontally at an altitude of 490m and having a velocity of 250m/s, drops a supply package to a work crew on the ground. It falls freely without a parachute.

What is the time required to hit the ground?

How far down range will the package travel before hitting the ground?

It helps to draw a simple diagram of the problem:

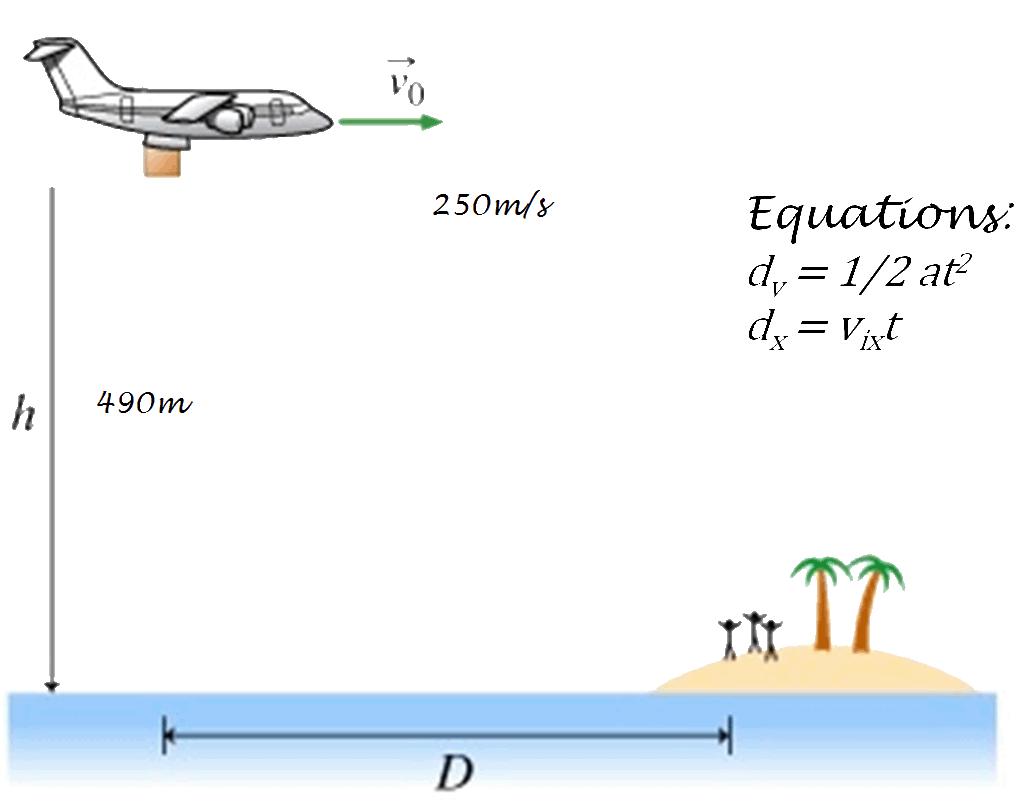
Practice problems:
Horizontally Launched Projectiles 1
Horizontally Launched Projectiles 2
Horizontally Launched Projectiles 3

Projectiles at an Angle

How to approach Projectiles at an angle:
Break it into two separate problems: a vertical free-fall problem and a horizontal d = vt problems.

You do this by breaking the initial velocity vector into its x- and y-components. From there it is nothing more than what has been covered earlier.

Example Problem:

Here is an example of solving a Projectile at an Angle kind of backwards so that you can see how it all comes together- a better understanding of how it works. If you would rather just get to the problems skip to there from here.

A ball is thrown straight upwards at a velocity of 22.9m/s. How long will it take to reach the top?
	Start with the usual v=at equation. Since we need to solve for t we change the equation around to this.
Side note (well, a semi-side note): Why use v = at instead of the version in the Reference Tables: vf = vi + at? If you were to use the longer, more formal version you would need to use and keep track of positives (+) and negatives (-). At which point, for this situation, you would end up having the equation 0 = vi + at. Then you would have to move the vi to the other side of the equal sign to solve for t. Since one value is zero, you can use the simpler version which actually solves for the trip down. It takes the same amount of time to go up as it does to come down so the math works out to be the same.
	Plug in your values and calculate.
	The t here represents how much time it takes for the ball to reach the top.
What is the height at the top?
	The equation we use now is dy = ½at2 (In the original d = vit + ½at2 the vi becomes zero and this term drops out). We don’t use d = v/t because in this situation v is constantly changing.
dy=(.5)(9.81m/s2)(2.33s)2 =26.6m	Substitute the values and crunch the numbers.
How far will a ball travel if shot at 32.7m/s horizontally and travels for 2.33s?
	We want to find the distance in the x-direction (horizontal) so we start with v = d/t but change it to solve for d: d = vt.
dx = (32.7m/s)(2.33s) = 76.2m	Substitute the values and crunch the numbers.
Put the vertical and horizontal together and you get a horizontally launched projectile. It falls down with the acceleration of gravity for 2.33 seconds and travels at constant velocity for the same amount of time to reach76.2m.
2.33s up and 2.33s down = 4.66s	The trip up takes the same amount of time it takes for the trip down. The round trip would take 4.66 seconds.
	As it is flying up, it travels horizontally for 76.2m. As it falls down it travels another 76.2m for a total horizontal distance of 152.4m.
What is the angle of launch?
Using trig, you can find angle θ by using the tangent- or more specifically: the arctangent (AKA inverse tangent or tan -1). SOH, CAH, TOA⇒ Tangent is opposite over Adjacent.
tanθ = 22.9⁄32.7	No units needed since they cancel out.
θ = tan-1(.70)	Rather than getting caught up in the tan-1 use and terminology, tan-1 simply means "what angle has this____ value?"
θ = 35˚	This is the launch angle.
What is the velocity of launch?
(32.7)2 + (22.9)2 = v2 v = 39.9m/s	The velocity of launch is a combination of the vertical and the horizontal speeds. By simply applying the Pythagorean Theorem you can calculate the hypotenuse: a2 + b2 = c2

Problem:

A football player kicks the ball at 25m/s at an angle of 53˚ above the horizontal. (use 10m/s² for g to make life easy)

• What is the vertical speed?
• horizontal speed?
• time to reach the peak?
• max height of the ball?
• time to peak and land (hang time)?
• total distance traveled (horizontal)?

Or you can just think of it this way:

Do all of your calculations for horizontal projectiles and double whatever gets doubled:
-time of flight
-distance of flight

What angle will give you the furthest shot?

45˚ will give you the best combination of hight and horizontal speed.

Angles that have the same spread from 45˚ (ex: 30˚ & 60˚ are each 15˚ away from 45˚) will land at the same spot. One will take the high road and the other will take the low road. The high road has a longer flight time but a lower horizontal speed while the opposite is true for the low angle.

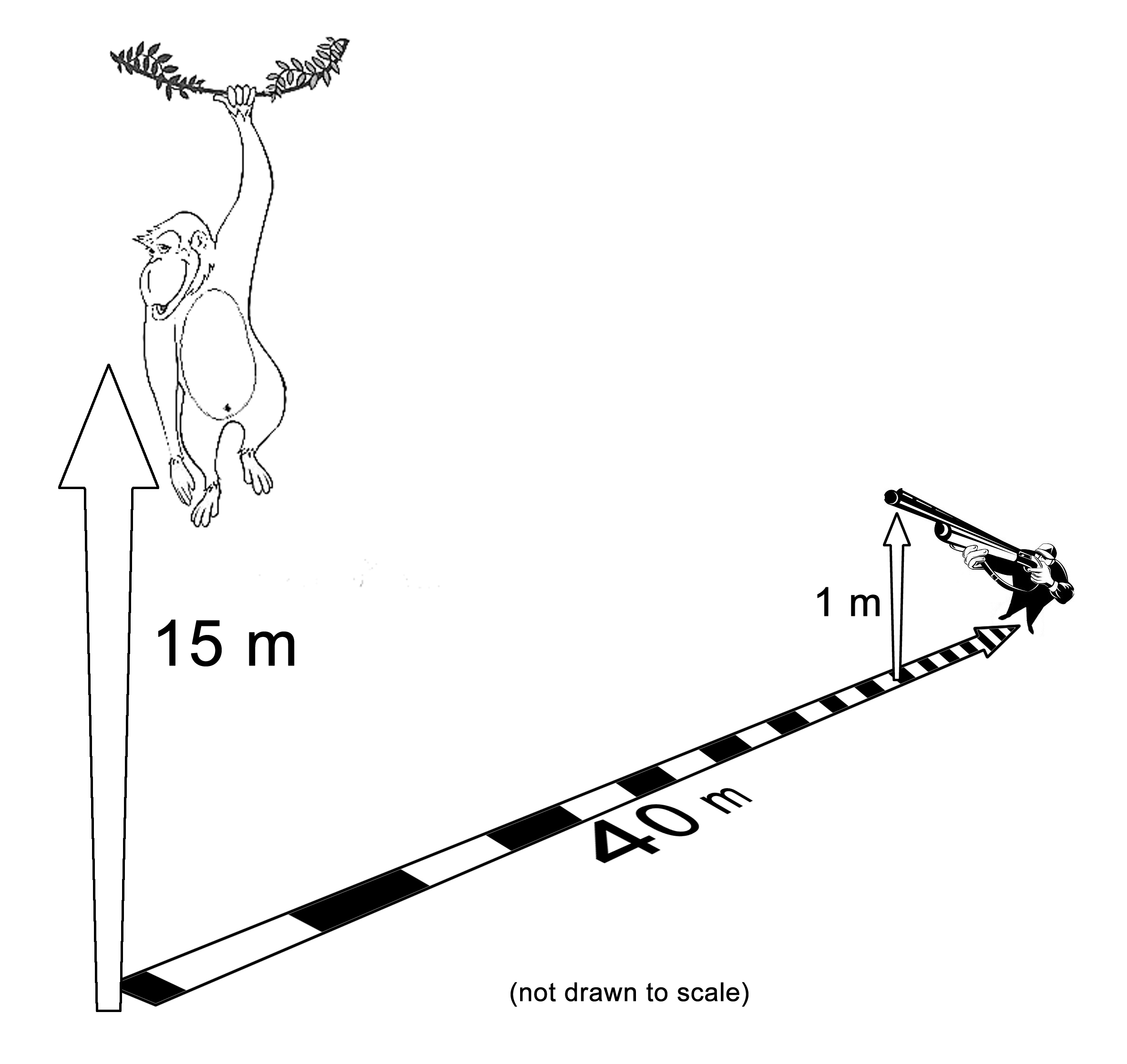
A Classic: The Hunter and the Monkey
	The hunter aims his Tippmann A-5 paintball gun directly at the monkey. At the exact moment that the gun fires the monkey lets go of the tree and falls. If the initial velocity of the Tournament Grade Empire Ultra Evil paintball is 30 m/s and the muzzle of the gun is 1 m above the ground. Will the bullet strike the monkey, pass over his head or go under his feet?
Do the trig
tanθ = 14m⁄40m θ = tan-1(.35) θ = 19.29˚	The first thing that we need to do is to figure out the angle of the hunter’s gun. The tangent of the unknown angle is equal to 14/40. Using the inverse tangent function will give us the angle of 19.29˚
vx = (cos19.29˚)(30m/s) = 28.31575m/s vy = (sin19.29˚)(30m/s) = 9.91049m/s	Find the x- and y-components of the paint ball’s velocity. Note on sig. figs: This is a mathematical exercise where you can assume that the values are mathematically accurate to an infinite number of decimal places. For the purposes of this exercise, it is necessary to minimize the impact of rounding. As such, I am being excessive with the sig figs.
How long will it take the paintball to cross the monkey's path as he drops?
d = 40m vx = d⁄t therefore; t = d⁄vx 40m⁄28.31575m/s = 1.41264 sec	To calculate the time, you take the horizontal distance from the hunter to the monkey and divide it by the horizontal speed.
Where (vertically) is the paint ball when it reaches the monkey’s path?
dy = vit + 1/2at2 = (9.914049m/s)(1.41264s) + ½(-9.81m/s2)(1.41264s)(1.41264s) = 14.00498m -9.78818m = 4.2168m above ground	Since we are searching for the vertical position we will use the vertical component of the paintball’s starting speed then factor in the acceleration of gravity downward. (Don’t forget the negative in front of the 9.81) Note: for this exercise the value of 9.81 was used for gravity. However, if you want to work it out with more precision you can use a value of 9.8039m/s2.
Where is the monkey when the bullet crosses the path?
dy = vit + ½at2 dy = ½at2 dy = (.5)(-9.81m/s2)(1.41264s)(1.41264s) = -9.7882m	We use the free-fall equation to see how far the monkey drops in the time we calculated for the paint ball to cross the monkey’s path. Since the monkey starts falling from rest, his initial velocity is zero and the first term drops out. The monkey dropped 9.7882m down from the tree.
14m – 9.7882m = 4.2118m	Since the monkey started at 14m above the ground and dropped 9.7882m under that, he was at 4.2118m above the ground at the same time the paint ball crossed his path.
The result? At the time that the paint ball crosses the Monkey's path - 1.41264 seconds after firing:
The Monkey is 4.2168m above the ground.	The paint ball is 4.2118m above the ground.
Both objects are at the same place at the same time (give or take a little due to rounding issues but close enough to hit the monkey).
SPLAT!
See a youtube demonstration of the Hunter and the Monkey: http://www.youtube.com/watch?v=cxvsHNRXLjw