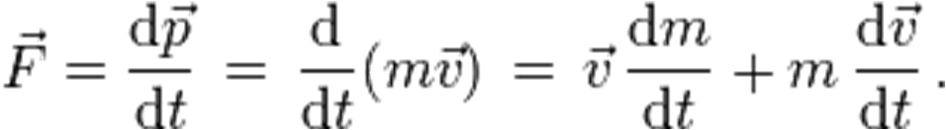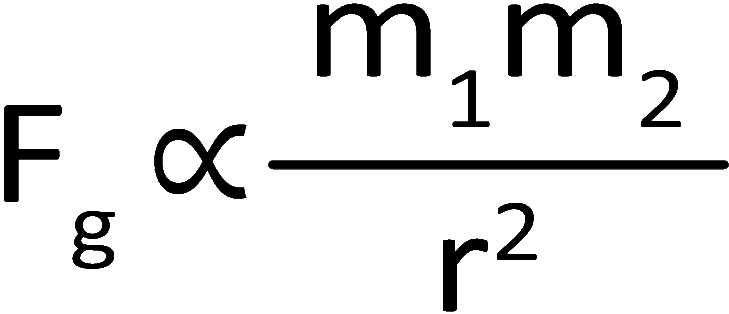Newton's Work
Newton’s LawsA little about Isaac Newton: Newton’s Three Laws of Motion: |
Speed Links These will take you to sections below: Worksheets |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Newton's 1st LawObjects in motion will stay in motion, objects at rest will stay at rest, as long as they are not acted upon by external forces (AKA: Net Force or Resultant Force).
An example of inertia in action: The car is in motion and wants to keep going in motion. The people are at rest and want to stay at rest. Inertia In Action ( http://www.wimp.com/brakinghard/)
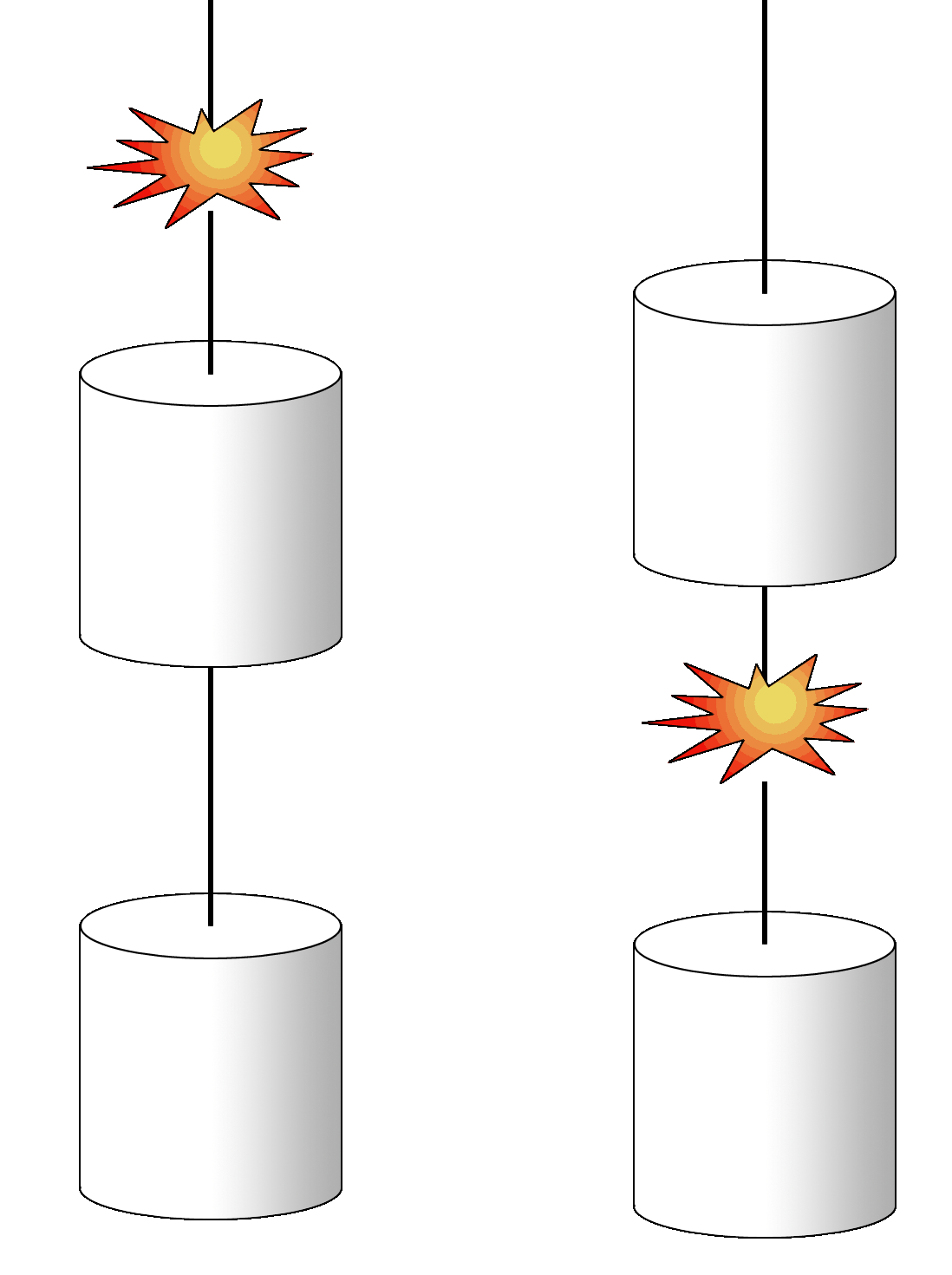
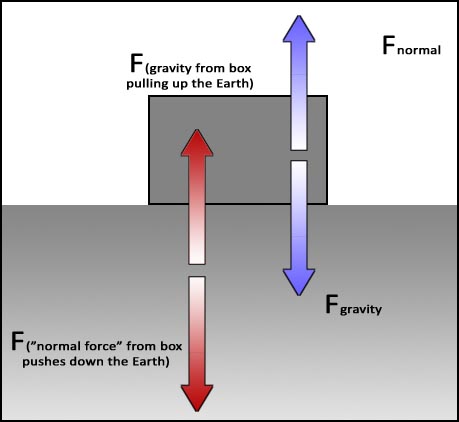
Newton's 3rd Law(I know I didn't do the 2nd yet but the 3rd goes along much better with the 1st. For every force there is an equal and opposite force (and the forces must act on separate objects).
Newton’s Second Law"The acceleration of an object is directly
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
a = F/m and F = ma F = (60kg)(9.81m/s2) =588.6kg•m/s2 =588.6N "For every force there is an equal and opposite force." |
|
aChuck Norris = F net /m
|
aEarth = F net /m
|
aChuck Norris= 588.6N /60kg
|
aEarth = 5.88N/6x1024kg
|
aChuck Norris = 9.81m/s2 (which is a measure of how much movement a person experiences |
aEarth = 9.81x10-24m/s2
|
Conclusion: Chuck Norris DOES push the Earth down! |
|
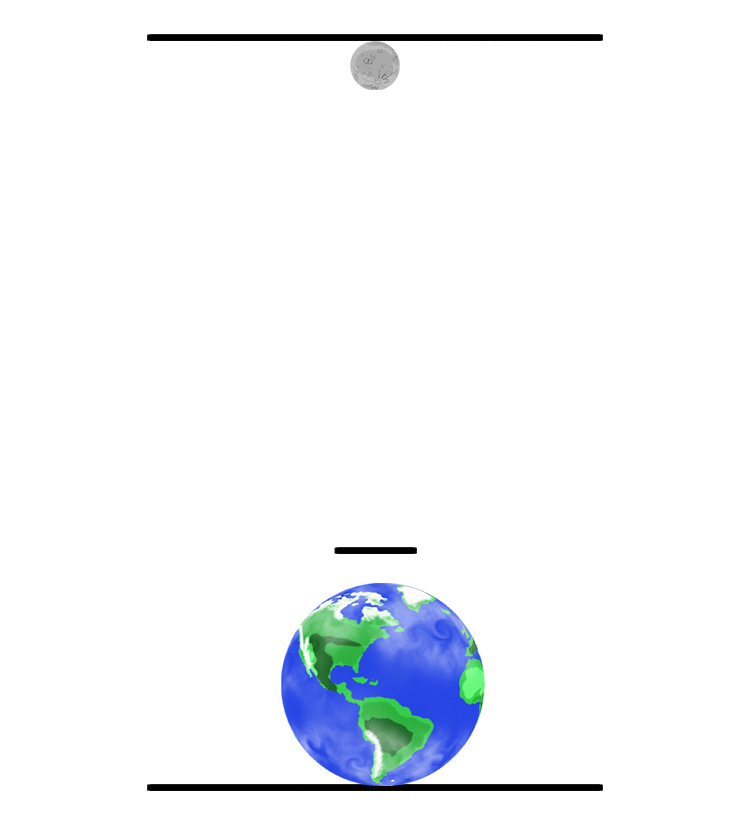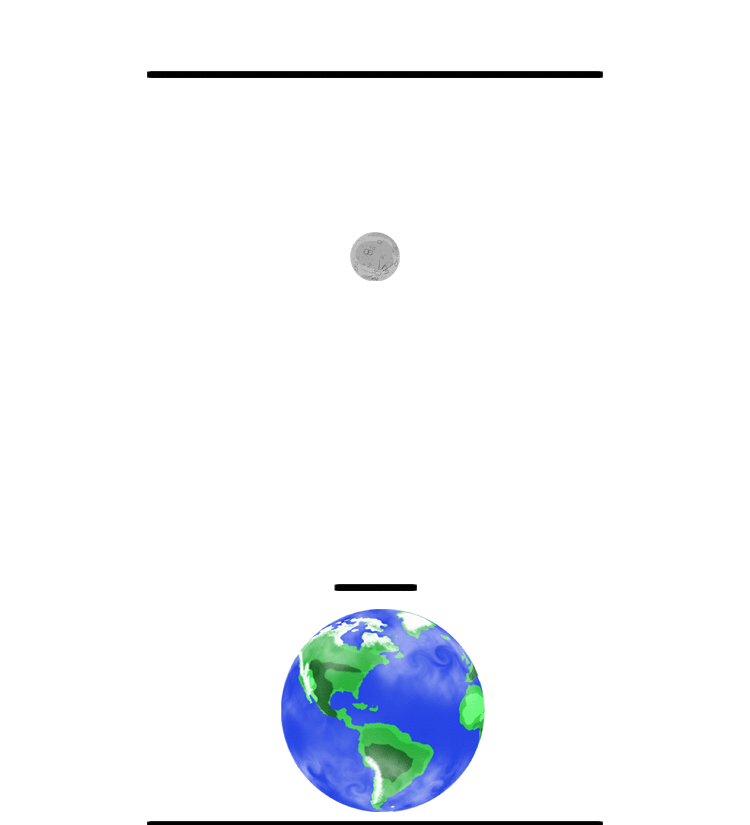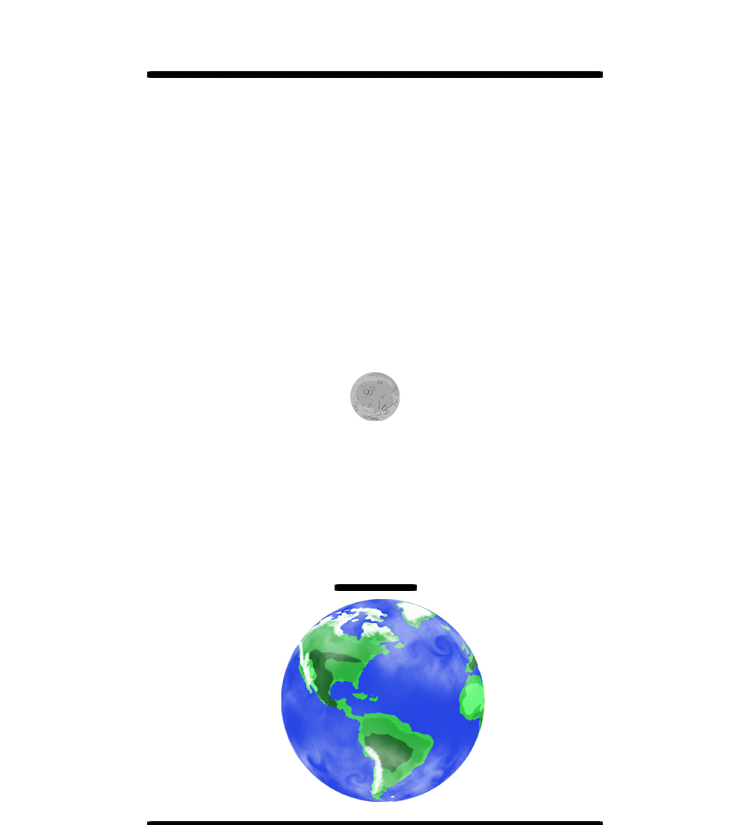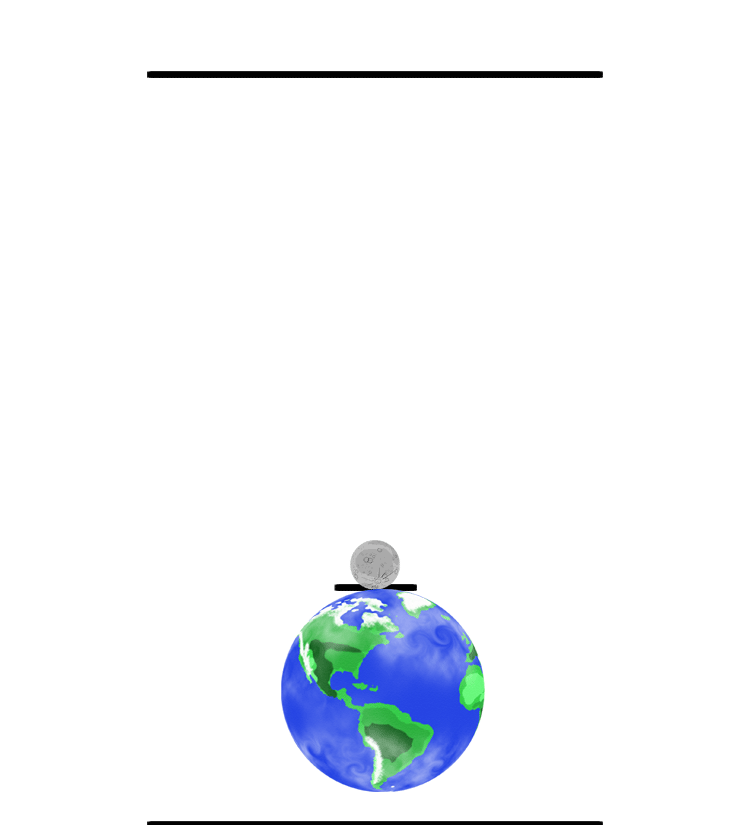 |
Both objects pull equally on each other. The force of gravity on the moon is exactly the same force that is on the Earth. However, since the Earth is so much more massive than the Moon, it moves much less (see math above as an example). The balance point between the Earth and moon (or any two bodies) is called the barycenter. The barycenter of the Earth-Moon system is located inside the Earth about 1707 kilometers (1,060 miles) below the surface. (The animation to the left is not drawn to scale, hence the center point of the system is outside the Earth.) Drawing and animation by Phil Medina |
Now look at this: See how the weight (hammer) does not simply revolve around the athlete but they revolve around each other. They both spin around their common balance point. Since the athletes are so much more massive than the hammer, the center of the two masses is much closer to the athlete. Hence, the athlete makes small circles and the hammer makes much bigger circles- just like the Earth and Moon revolving around each other.
|
|
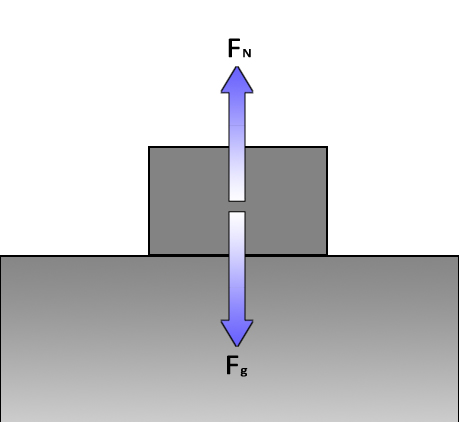
The Normal ForceThe Normal Force (usually shown as FN but sometimes simply as N) is a reactionary force that a surface will produce to oppose a force pushing on it. The term "normal" comes from the geometric term referring to “perpendicular to”. The normal force will always be perpendicular to the surface (which is not always opposite to the direction of gravity). At first thought, it may seem that the normal force is some made-up abstract concept, but if the normal force and the force of gravity (in the example above) were not equal in strength then the block would move vertically- up if the normal force somehow is greater and down if the normal force was not enough to balance the gravitational pull. If that was the case, the surface would not be strong enough to stop the weight of the box and it will break allowing the box to fall. |
|
 |
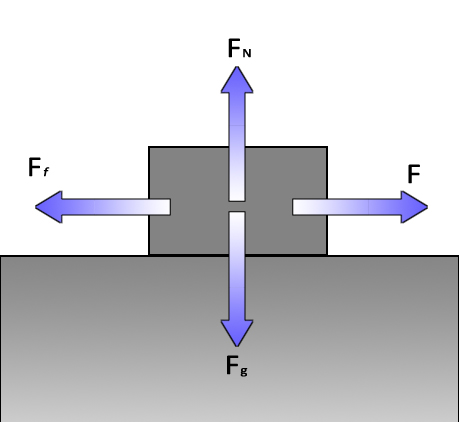
An object in constant motion (or at rest): A block moving at a constant speed may have the same exact free body diagram as an object at rest (above) or may have equal and opposing forces working on it since "objects at rest will stay at rest and objects in motion will stay in motion AS LONG AS FORCES ARE BALANCED." |
 |
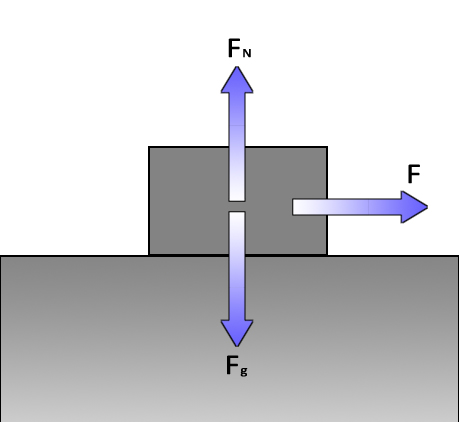
An object in constant motion with friction: Vertical forces are equal and opposite: no movement (or change in movement) up or down. Friction resists motion and slows objects down. To keep the speed constant, a force must be applied to cancel out the effect of friction. A common example of this is maintaining speed in a car. If there were no friction, once the car gets up to highway speed, say 55mph, you should be able to take your foot off the gas and coast at 55mph forever. But because of ground friction and air friction (drag) you need ot apply a little gas in order to cancel out the friction. |
 |
A block being pulled by a string on a frictionless surface: Vertical forces are balanced. |
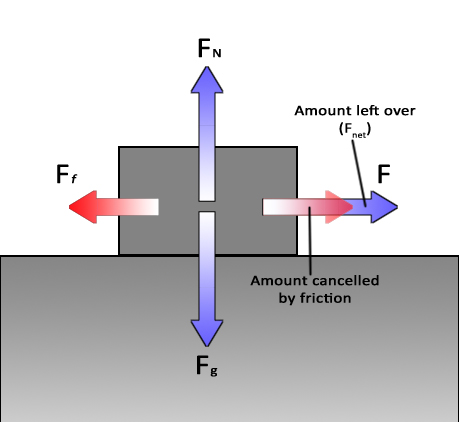 |
A block being accelerated by a string with friction: Vertical forces are balanced. The force of the pull is greater than the force of friction. Some of the pull is cancelled out by the friction, but the pull to the right has some force left over which is used to accelerate the block. The leftover pulling force is called the Net Force (Fnet). |
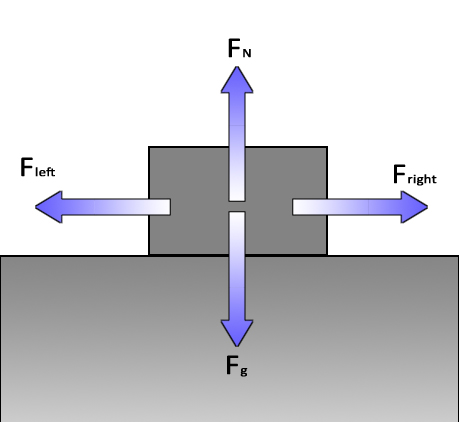
Net ForceIf there are two equal forces that act in opposite directions, they will cancel each other out or balance. If one force is greater than the other, they only partially cancel each other out. Any remaining force is called the net force (Fnet) which will then be used to accelerate the object. |
|
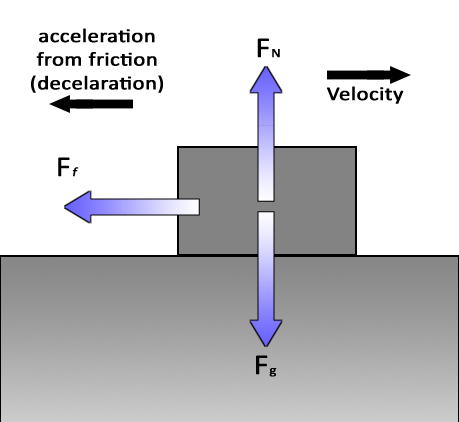 |
A block moving to the right and sliding to a stop due to friction: In this case, there is no force or push to the right. The block is moving due to its own inertia. On a frictionless surface, it would continue at constant speed forever. However, friction adds a slowing force which causes an acceleration to the left (sometimes called a deceleration). |
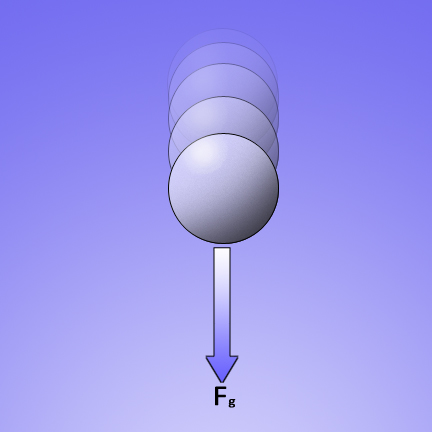 |
An object in free fall: The term "free fall" refers to the object being free to fall. In other words nothing except gravity is working on the object. This object has the gravitational force pulling it down and no other forces working on it. (On Earth, in reality, there will be air resistance but “this is your world, you can do what you want” – Bob Ross 1:46.) |
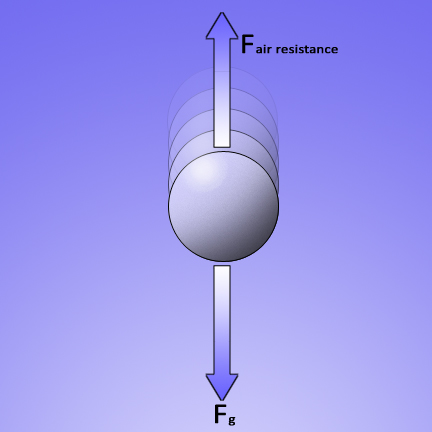 |
An object falling at terminal velocity: The object falls through the air so fast that the air can no longer get out of the way fast enough. The resistance of pushing through the air equals the force of gravity pulling down. The two forces cancel each other out and the object stops accelerating. It has reached “terminal velocity” which is the fastest that the object can fall. |
| Life on an Elevator worksheet | |
|
When the force applied to an object is at an angle, the diagonal force must be broken into horizontal and vertical components so that they can be compared to other forces working on the object. To break the diagonal force into horizontal and vertical components, you need to use trigonometric functions to figure out the sides of a right triangle. Critical to this, are the sine, cosine, and tangent functions. |
||||||
Sample Problem:A force of 18N is applied to a lawnmower at a downward angle of 27˚. The lawnmower has a mass of 10kg and the force of friction holding the lawnmower back is 11N (we will discuss how to calculate the force of friction later). What is the acceleration of the lawnmower? |
|||||||
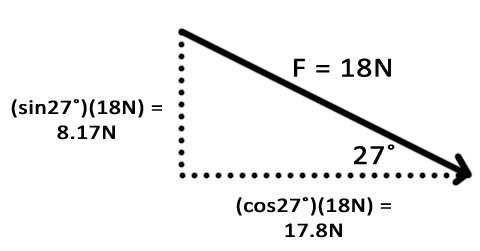 |
If a force of 18N is pushing down at an angle of 27˚, it would be just the same as two separate forces: Fy = 8.17N straight down and Fx =17.8N horizontally acting at the same time. These are the X- and Y- components. Much the same way that you cannot draw a straight diagonla line with an Etch-A-Sketch, You need to go up a little, then over a little, then up a little, then over a little, then up a little, then over a little, then up a little, then over a little, then up a little, then over a little, then up a little, then over a little, then up a little, then over a little, then up a little. Then you did two ups in a row and you messed the whole thing up and have to start over. But your sister wanted a turn so she pulls it away from you and you never get to make the perfect diamond shape on your Etch-A-Sketch. |
||||||
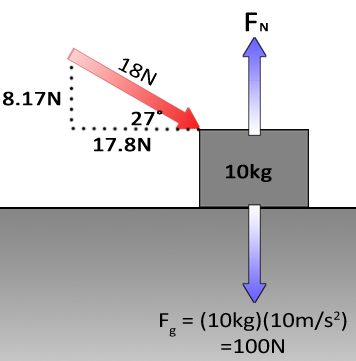 |
When the force is applied to a box (or a lawnmower), you will see the applied force (diagonal vector) gets split into the vertical and horizontal forces. Considering just the vertical component (8.7N down) it "adds to" the weight of the box. In other words, the downward force is 100N from the box and another 8.7N from the downward push. The total downward force is 100N + 8.7N or 108.7N down. |
||||||
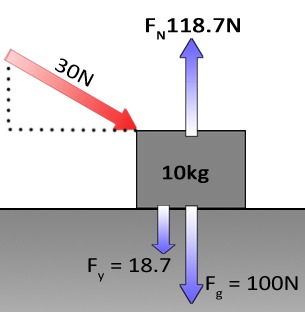 |
The normal force will oppose and equal this force bringing that value also to 108.7N up. |
||||||
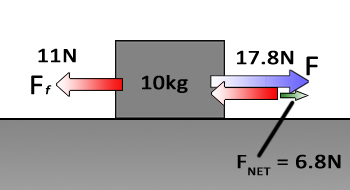 |
Now for the horizontal forces: The push has a horizontal component of 17.8N to the right (or +17.8N). This is opposed by the Force of friction (Ff) of 11N to the left (or -11N). This gives a Net Force (FNET) of 17.8N-11N = 6.8N. |
||||||
a = F/m |
Acceleration is Force (Net Force) divided by mass. (6.8k·gm/s2) / (10kg) =.68m/s2 |
||||||
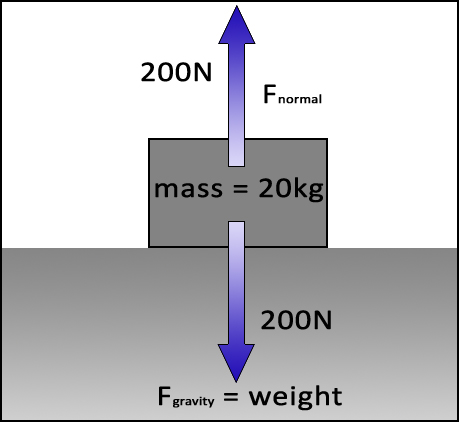 |
This is a free-body diagram of a box resting on a surface. The weight of the box is pushing down while the surface pushes back up at an equal force. The box is in equilibrium. Otherwise, if the two forces were out of balance you would get movement up (bouncing) or down (breaking through the surface). |
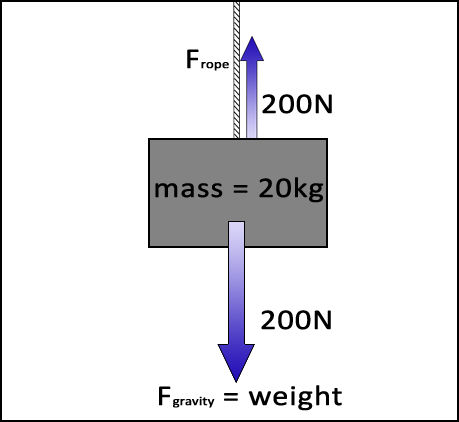 |
Now, if you remove the surface and, instead, keep the box in equilibrium by using a rope with an upward tension. |
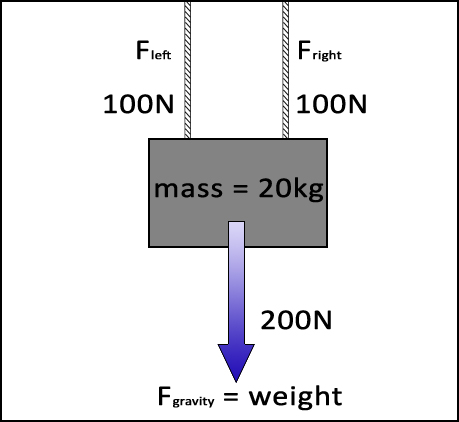 |
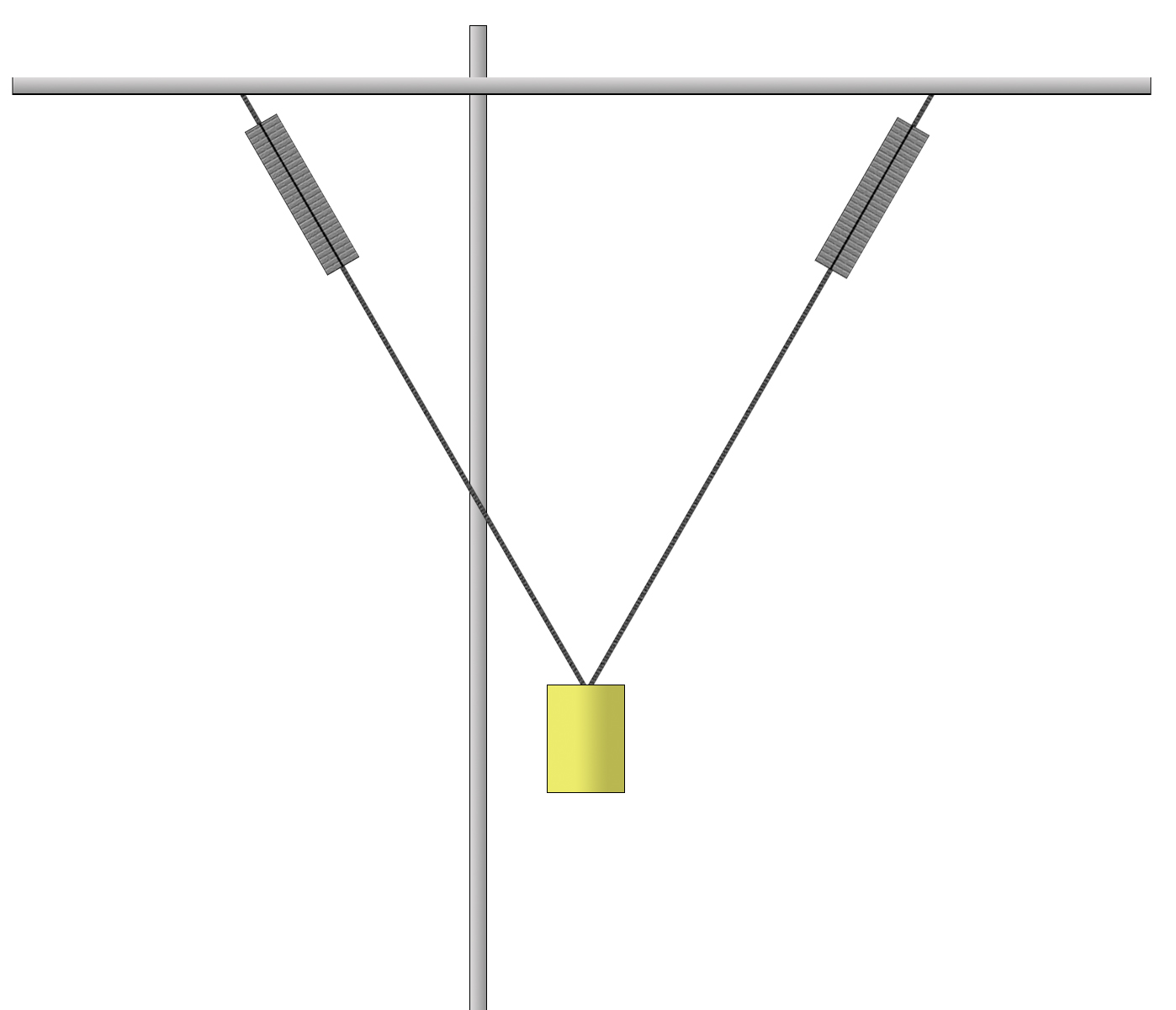
Take the rope and replace it with two ropes. Each rope will support 100N of weight to total the weight of the box: 200N. |
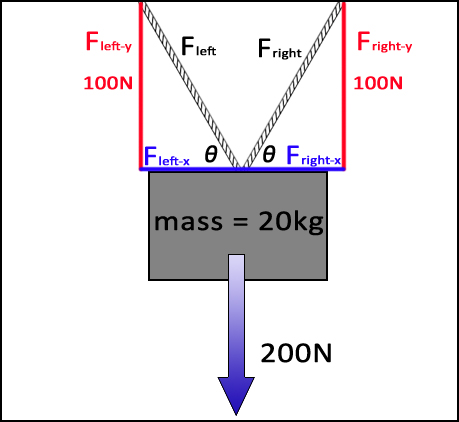 |
If the ropes are angled and the box is to remain stationary then the sum of all forces, vertical and horizontal, must still equal zero.
Whenever you see something angled in physics, you can bet that you will need to divide it into x- and y-components.Using trig and the known VERTICAL values (each rope has 100N) and one other component of the triangle (angle θ or Fx) you can then calculate the remaining values. In a regular right triangle x2 + y2 = hypotenuse2. Or, in this case: Fx2 + Fy2 = F2. Therefore, using trig: Frope•cosθ = Fx and Frope•sinθ = Fy. For this problem, we will use 30˚ from the horizontal for the angle of the ropes (not drawn to scale) .
|
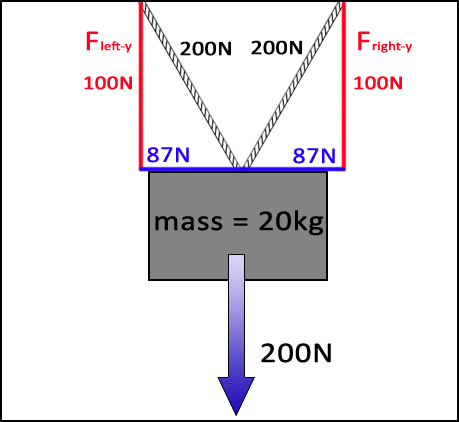 |
Since we know Fy (the vertical component that supports 100N on each rope in red) and the angle (for this problem we are given 30˚) we can calculate Frope using: Frope = 100N⁄sin30˚ Frope = 200N Once we have Frope, we can easily calculate Fx with: Fx = Frope•cos30˚ Fx = 87N These calculations are only to solve the forces on one rope. To get the other rope, simply copy the forces- no additional math is needed. Note: For this problem the force on the rope is 200N. It is NOT ALWAYS double the vertical force. It just works out that way for this problem because sin 30˚= .5 (dividing by .5 is the same as doubling). |
Static Equilibrium Lab(here's the write-up: Static Equilibrium Lab) |
|
 |
|
Sliding on Surfaces and Inclined Planes |
|
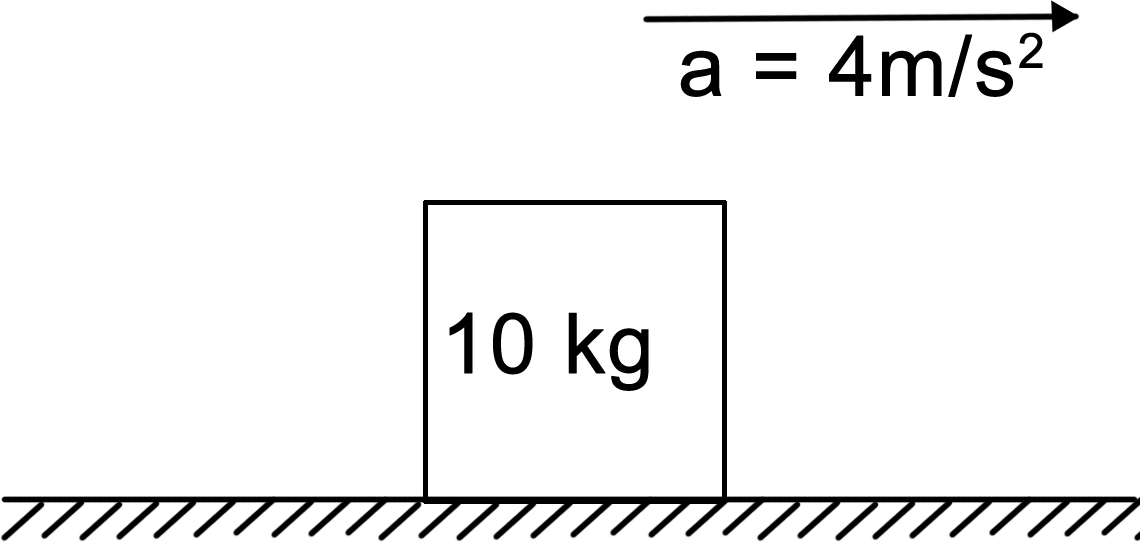 |
Problem: A 10kg block is on a frictionless surface. What is the tension (force) on the string? |
a = F⁄m⇒ F = ma F = (10kg) (4m/s2) F = 40kg•m/s2 |
Newton’s 1st: Objects will continue doing what they are doing unless there is an unbalanced force (net force). Since the object is accelerating, there must be an unbalanced force provided by the string. This is a frictionless surface and the string does not need to overcome friction. Therefore, all of the string’s tension directly produces the acceleration. Vertical forces are ignored since they balance and cancel. |
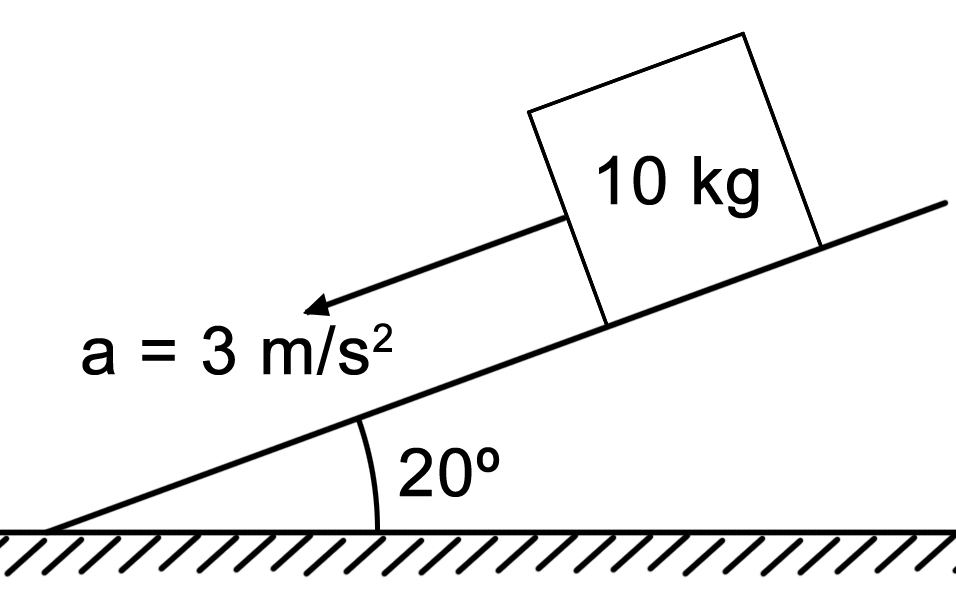 |
The Problem: A 10kg block slides down a 20˚ incline and accelerates at a rate of 3m/s2. What is the force of friction? |
Here are those pesky angles again. Of course, if you have an angle you have to break it into its components. BUT! There’s a huge difference between having one force at a diagonal and having three forces at an angle (force down the incline, up the incline and the Normal Force perpendicular up from the plane). With the inclined plane problem, notice that all the forces except weight are perpendicular to each other. |
|
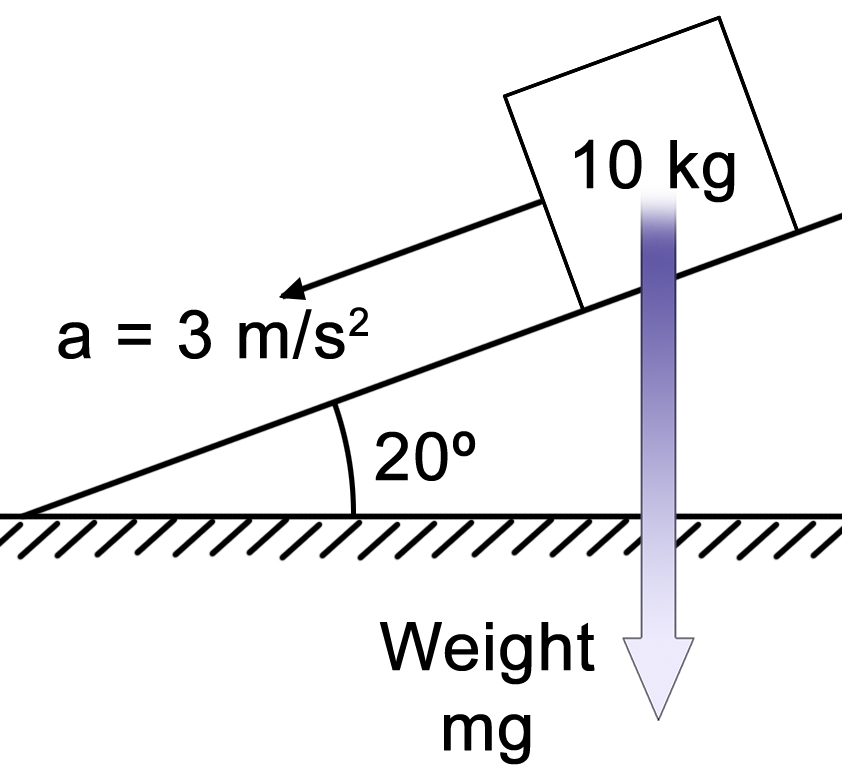 |
The hard way: resolve each of those three forces into their components so that they are at right angles to the weight. Easy way: resolve only one force- gravity- into components that are perpendicular to all the others. I choose the easy way because it is easier. First step: Gravity and weight are straight down towards the center of the Earth- NOT “straight down” into the plane. |
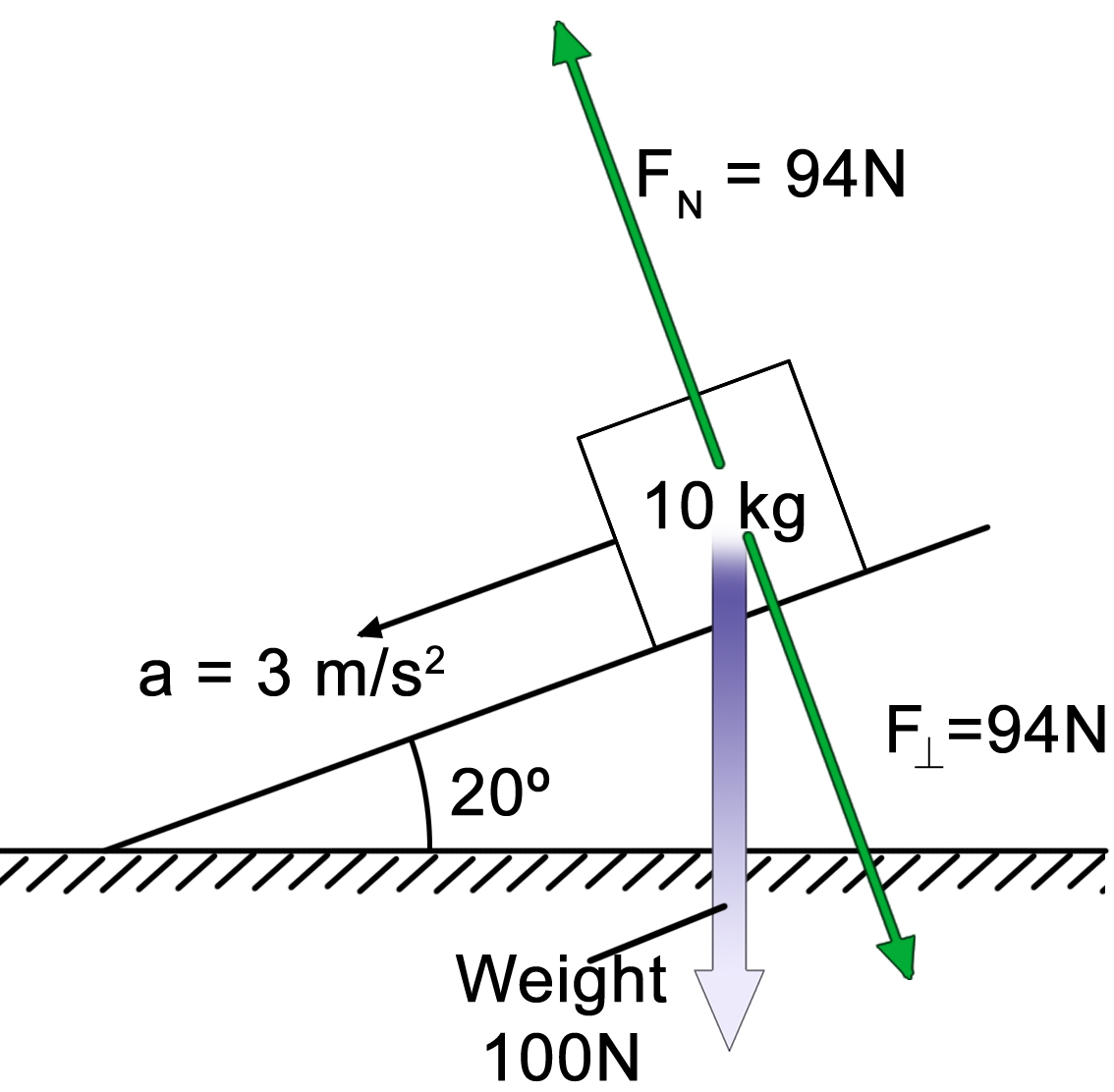 |
Next step: resolve weight into components that are perpendicular and parallel to the surface. Weight will have a component that is perpendicular to the surface. By relationships of similar triangles the angle of the plane is the same angle that the weight makes with the perpendicular component. (Too much typing to explain it- just believe me ok?) In short: the angle between the weight and F⊥ is the same as the angle of the ramp. We are making a right triangle with the hypotenuse being the weight and on leg the perpendicular force. The value of the perpendicular force is: F⊥ = (100N)(cos20˚) = 94N This means that the block has 94N worth of force pushing directly (right angle) into the surface. As a result, the normal force pushes up PERPENDICULAR TO THE SURFACE also with 94N. To solve this problem, we do not need this value but it will really become important when we have to calculate the force of friction.
|
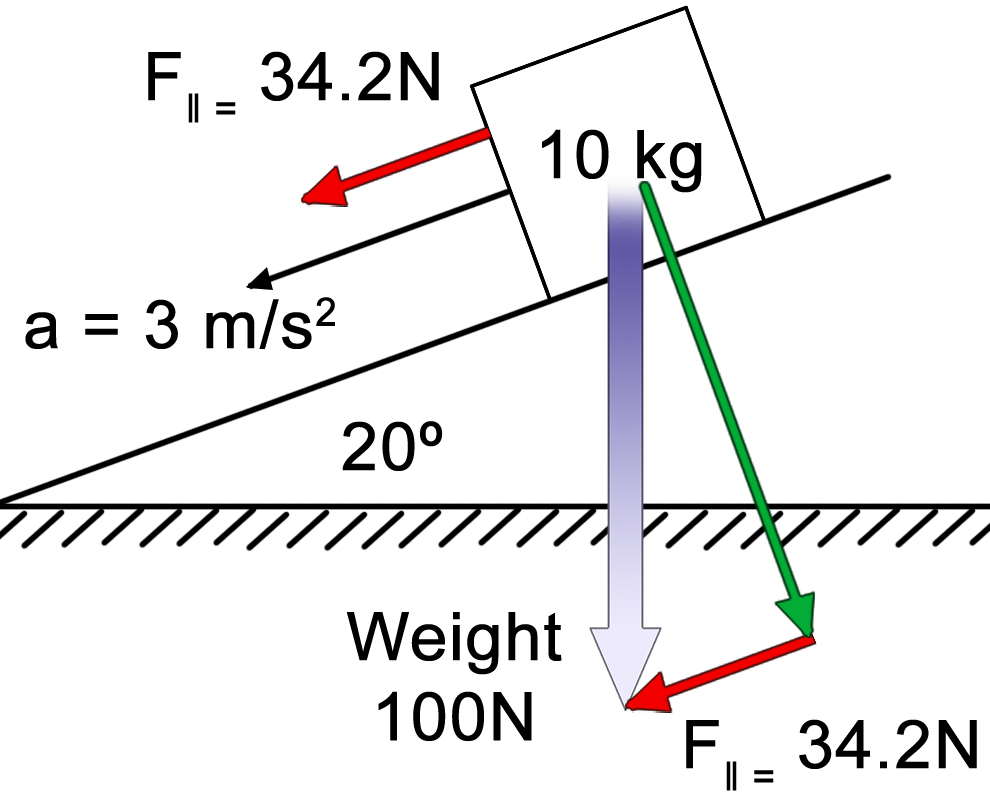 |
For the force parallel (F∥) to the plane’s surface, we use (100N)(sin30˚). Although this is often drawn and calculated below the plane’s surface, it actually represents the downward force along the plane from the box’s center point. Which is why it is shown in both places. They are one and the same force. |
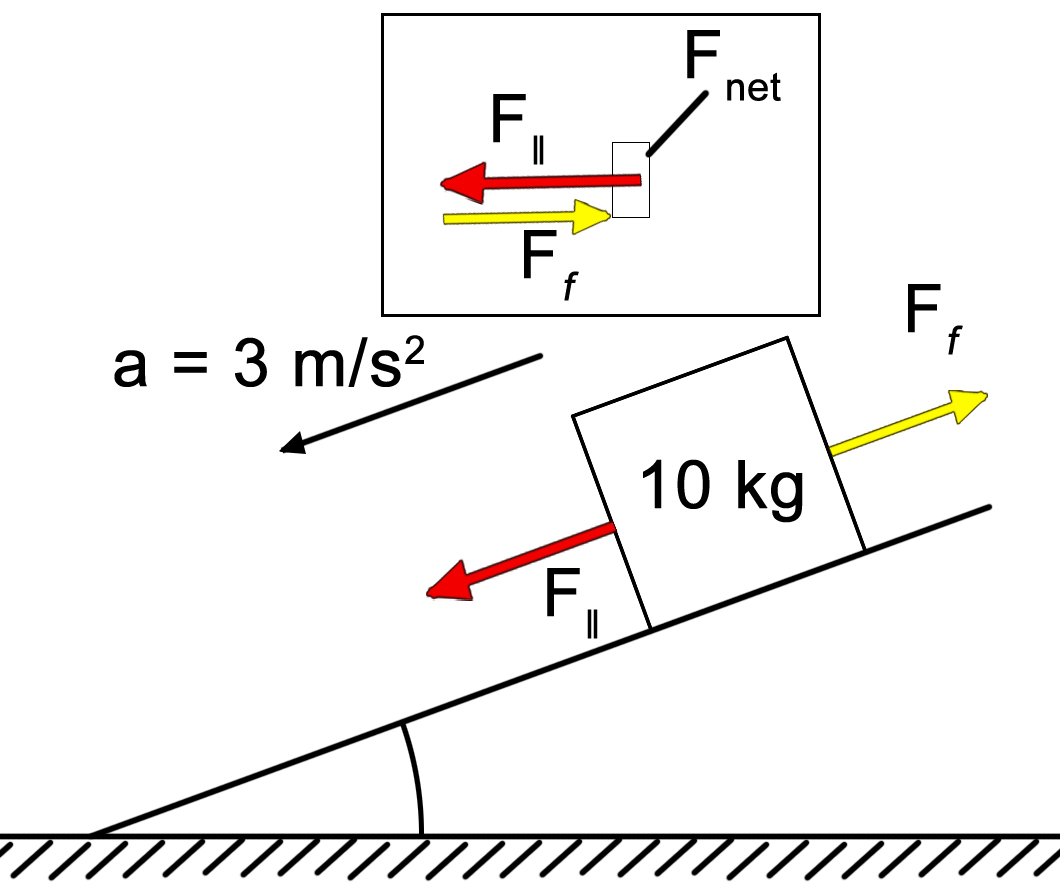 |
Let’s take inventory:
We have 34.2N of force pulling the box down the incline. See insert: 34.2N - 30N = 4.2N |
ANSWER: The force of friction is 4.2N up the plane. |
|
Friction
Calculating the Force of FrictionFriction is a gripping force between two surfaces that are in contact with each other. At the microscopic level, even smooth surfaces have pits and bumps. These bumps act like Velcro™ and the surfaces lock into each other.
|
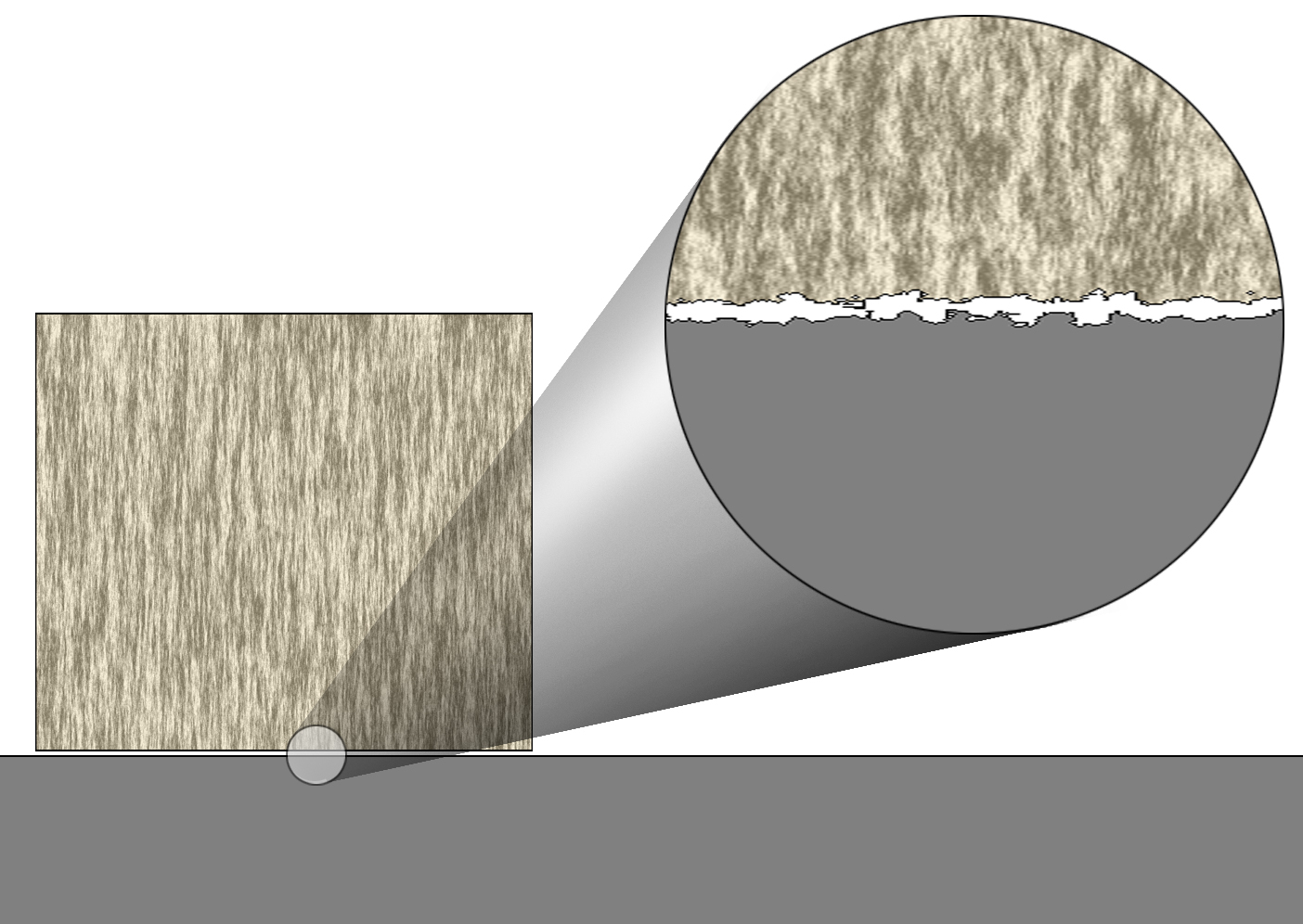 |
There are two kinds of friction that work between surfaces: static and kinetic. Static friction is between two surfaces that are at rest together- they are not sliding over each other. This type of friction is stronger than kinetic because the bumps of each surface have a chance to settle into each other and really get a good grip. Kinetic friction is between two surfaces that are sliding past each other. This friction is weaker because the bumps of one surface skip over the bumps of the other and do not have a chance to settle into each other to strengthen their bond. The difference between these two types of friction can be demonstrated by moving a refrigerator across the kitchen (so that you can vacuum the heat dissipating coils in the back to increase efficiency and prevent fires). When you first push the fridge, it is very difficult to get moving. Once it starts to move, the pushing is not as hard. The coefficient of friction (stickiness factor) with the symbol μ (Greek letter mu) is a value for the stickiness of the surfaces. Since it is an interaction between two surfaces, μ is specific only to each two surfaces that are in contact. For example, μ for a rubber tire on ice will be different than a waxed ski on ice. The force of friction depends on the stickiness between the two surfaces and how hard the two objects are pressed together. It is calculated using Ff = μFN |
|
Newton's Universal Law of GravitationIf you were to just guess about what makes gravity's pull stronger or weaker, you probably would have no problem saying that gravity would be stronger when the objects are bigger (more mass). You would also probably say that gravity would be weaker if the two objects were farther away. |
|
Mathematically speaking, you came up with the equation to the right. To read this: "the force of gravity is directly proportional to the masses of the two objects and inversely proportional to the radius." Note: radius does not mean how big the Earth or moon or whatever is. It means the distance between the two objects. It is referred to as "radius" because it can be the distance in any direction- such as the radius of a circle. |
|
Directly proportional: in other words, if the masses get bigger, the force would get bigger. |
|
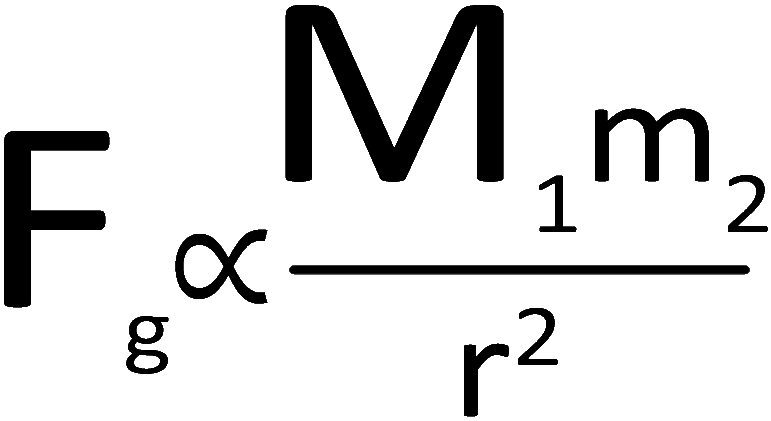 |
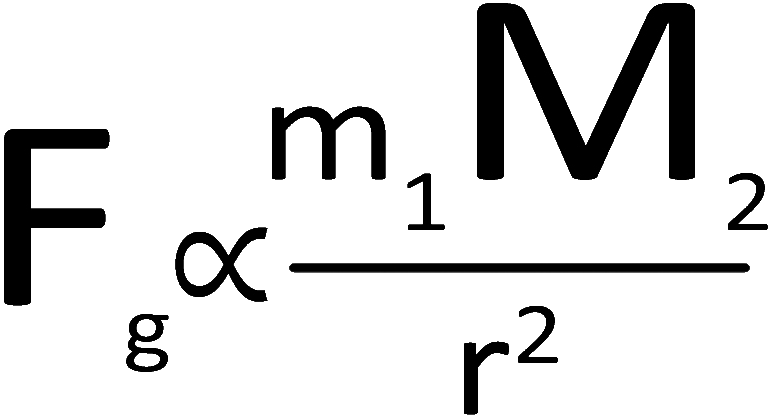 |
Inversely proportional means that as one gets bigger, the other one gets smaller. |
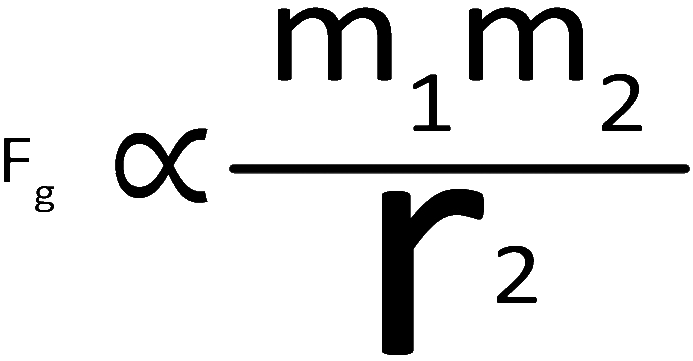 |
The reason why the radius is squared is because as you double the distance, the effects of gravity get spread over a larger area. Similar to how the circle from a flashlight will get weaker as you walk away from the wall. |
|
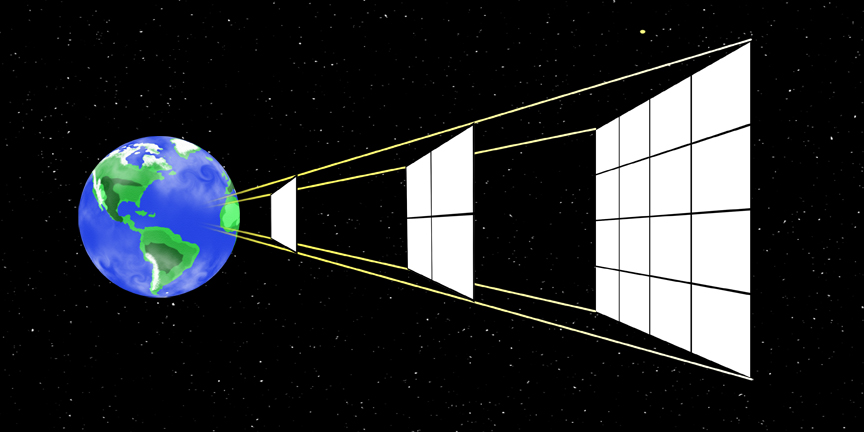 Original drawing by Phil Medina |
|
Or similarly: When Barney gets doused by a hose. If he is closer, he gets a stronger rush of water. As he increases his distance, the strength gets weaker. |
|
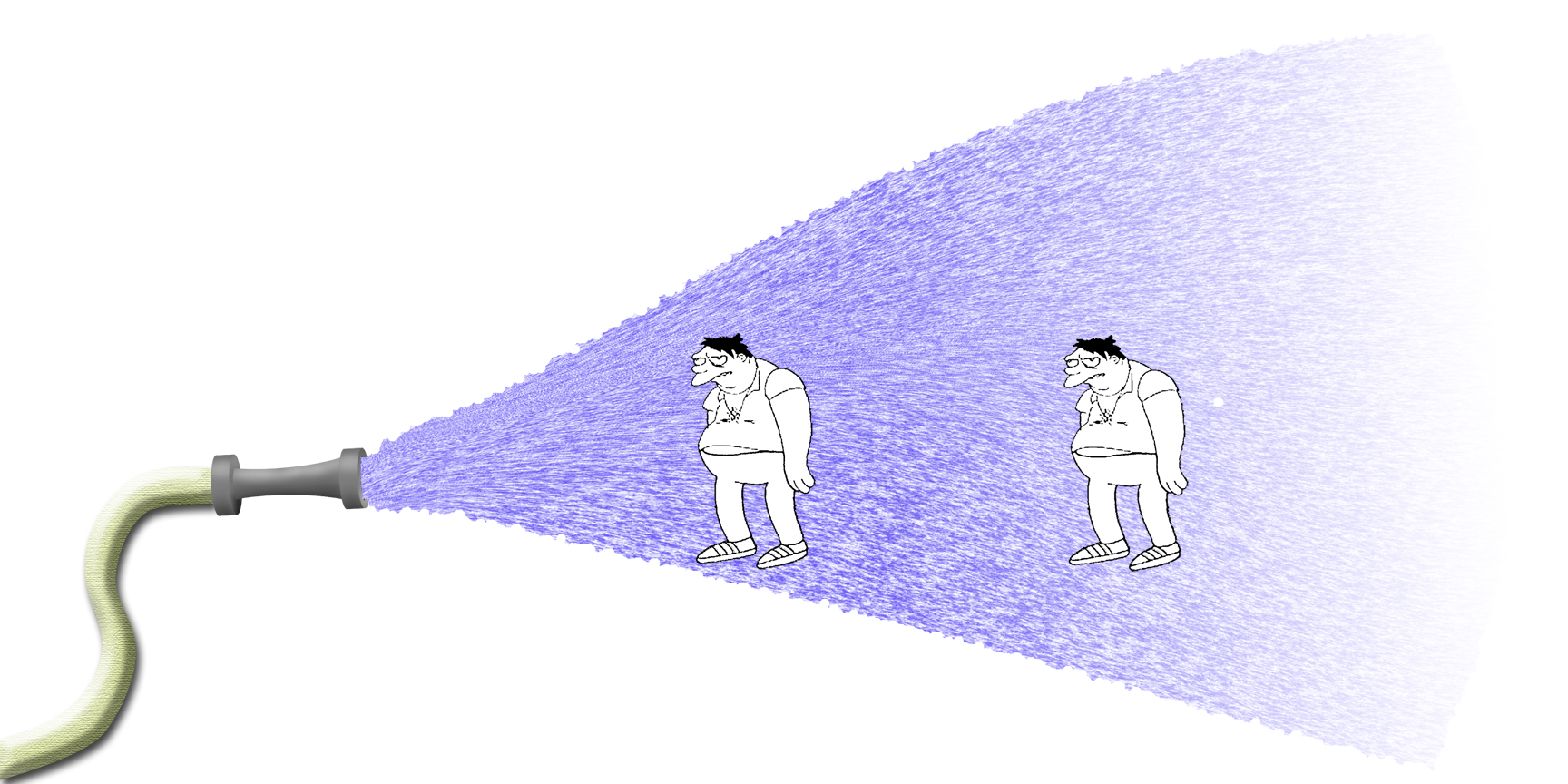 |
|
Now, if you were do some calculations using the proportions above you’d end up with some rather super-strong forces for gravity when, in fact, gravity is a rather weak force. It is only strong enough to keep you stuck to the ground because you have the entire pulling clout of the entire Earth – all 6 billion-billion-billion-billion (1024) kilograms of it. In order for the values to agree with what is really measured, we must be able to adjust the volume of gravity. So we use a conversion factor. Whatever value you calculate for the strength of gravity, you need to tone it down by a factor of about 11 orders of magnitude. In other words, divide it by roughly 100,000,000,000 (100 billion). The name for this conversion factor has a rather grandiose title: THE UNIVERSAL GRAVITATIONAL CONSTANT! CONSTANT! Constant! Constant! |
|
And it has a value of 6.67 x 10-11 N•m2/kg2. But that gets to be a bit cumbersome to constantly write over and over and easy to get lost in all the numbers and exponents and units. So it is simply represented by “G” until it comes time to actually crunch numbers. |
G = 6.67 x 10-11 N•m2/kg2 |
G. What's That?
One “g” is the acceleration of gravity (9.81m/s2). Standing still on Earth, you are experiencing 1g. If you accelerate faster than gravity’s acceleration you experience “multiple g’s”.
Experiencing 2g’s, you would feel twice as heavy as you normally would be.
10g’s you’d feel ten x your weight.
Fighter pilots can experience 10g’s for short periods. At that acceleration they would need to hold their arms up on the control stick as if their arm was holding up 71 pound weights as they did so.
Examples of G’s:
- Kingda Ka at Six Flags NJ: 2.9g’s
http://www.youtube.com/watch?v=HN8nv4tVFuA - Dodonpa Roller Coaster in Japan- highest g-rating on a coaster: 2.7g’s
http://www.youtube.com/watch?v=uvJRY7nOEQ0 - Space Shuttle launch; 3g’s
- Normal tolerance in humans before passing out: 5g’s
http://www.youtube.com/watch?v=znlBMHFdCEY&feature=fvwrel - Reentry of an Apollo capsule: 7g’s
Armageddon high G burn around the moon (fiction) 12g's with excessive g's for 11 minutes (and not one person passed out!)
http://www.flickclip.com/flicks/armageddon4.html - Car crash survivability limit: 100g’s for a brief moment.
The only person that has ever lived who may be close in
awesomeness
to Chuck Norris is Jack Bauer‡.

‡JackBauerFacts .com
With the exception of Chuck Norris and Jack Bauer, all illustrations were drawn by Phil Medina.
(No mere human can capture the essence of Jack Bauer or Chuck Norris so the image of Chuck Norris was drawn by Jack Bauer and the picture of Jack Bauer was taken by Chuck Norris.)

Over fifteen years of
Medina On-Line
1994-2011