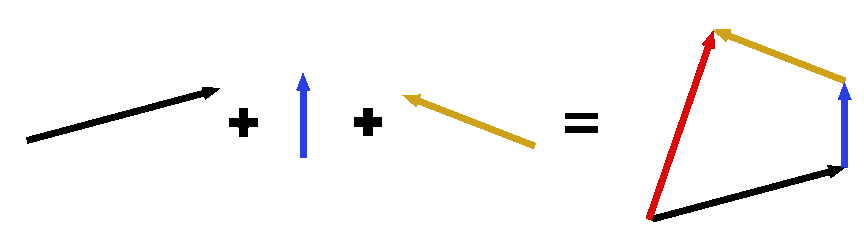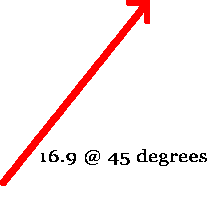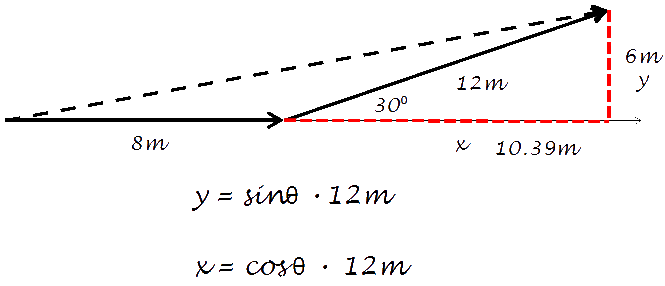Will it speed up or slow down?

Establish which direction represents + or -

6 5 4 3 2 1 0 1 2 3 4 5 6
-<------------------------>+

Scalar quantities have magnitude only.

Examples:
Time
Mass
Speed

Vector quantities have magnitude AND direction

Examples
Velocity
Acceleration
Force

Velocity: speed and direction (20 m/s, North)

Anatomy of a Vector

Tail	Head

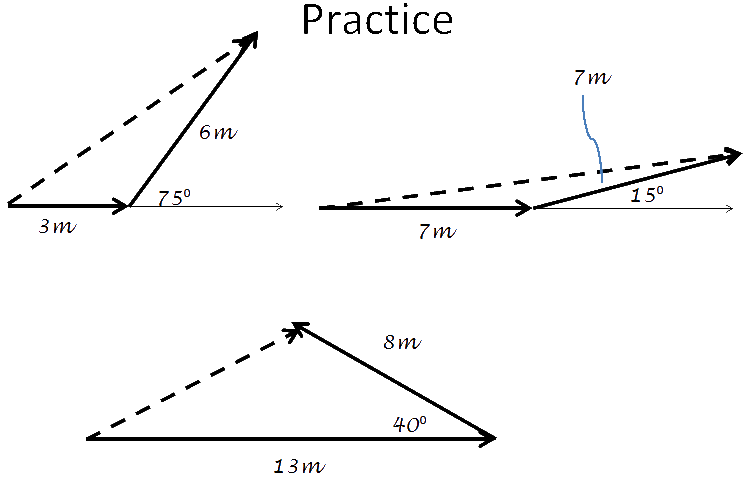
Vectors should be drawn to scale:

5m

10m

10 m should be twice as long as 5 m

Vectors get added “head to tail”(or “tail to head”)

5m	10m
15m
Resultant Vector

Adding vectors is the same as connecting them head-to-tail.
The resultant vector will be from the tail of the first one to the head of the last one.

Speed Links

River Problems

Worksheets

Compatability Pack for converting docx files to doc files

Graphically Adding Vectors

River Vectors
worksheet 1

River Vectors worksheet 2

River Vectors worksheet 3

River Vectors Homework 1

River Vectors Homework 2

A vector contains a magnitude (length of the arrow which is the value of whatever
the vector represents) and a direction. The direction is shown as the angle of
the vector. It is either shown as the angle of the arrow if drawn to scale, or as a
number of degrees.

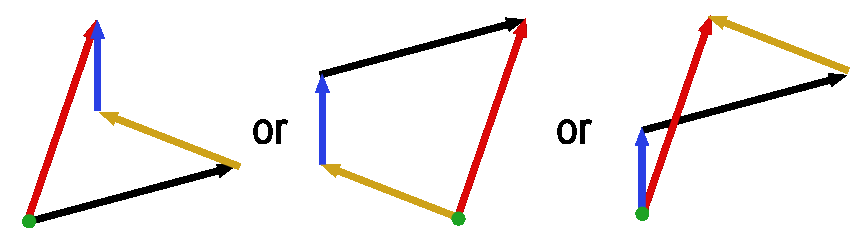
Adding multiple vectors will give you a single resultant vector (red).

It does not matter in which order you add the vectors. Regardless of how these vectors are added together, the red resultant vector will always be the same.

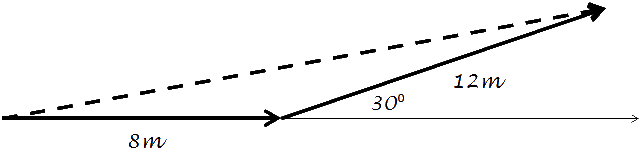
For example:

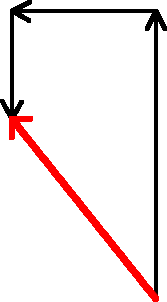
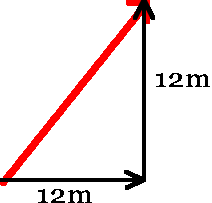
Graphically Adding Vectors worksheet

To calculate the resultant vector’s magnitude and direction:

If you can take two vectors at right angles and make a diagonal vector,
shouldn’t you be able to take a diagonal vector and make two right-angled vectors from it?

Can be:

What is the length of the resultant?

Separate the right vector into its x- and y- components.

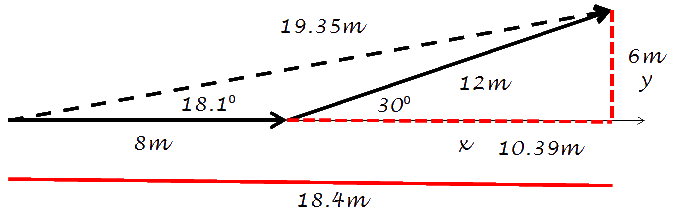
By adding the original 8m plus the horizontal component (x) of the angled vector,
you get the entire length of 18.4m.

Then using the vertical component (y) of 6m, you can get the length of the
resultant using a² + b² = c²

You can calculate the angle or the resultant vector by using the arc tangent of 6/18.4:
Angle = tan^-1(6/18)
Angle = 18.1˚

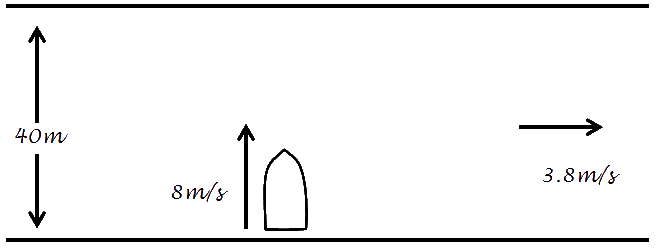
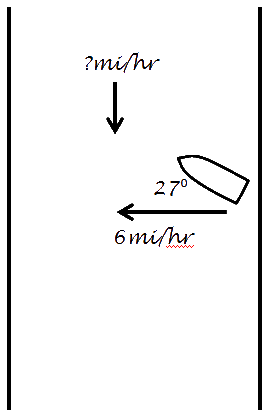
River Problems

Problem #1
A boat heads directly North across a river 40 meters wide at 8 m/s.
The current is flowing at 3.8 m/s to the East. (see diagram below)
a) What is the resultant velocity of the boat?
b) How far downstream is the boat when it reaches the other side?
c) How long does it take to cross the river?

a) Velocity is speed AND direction.
For speed: A² + B² = C²
(8m/s)² + (3.8m/s)² = C²
C = 8.8m/s

Velocity also includes the angle:
TOA: tanθ = opposite/adjacent
θ = tan^-1(3.8/8) = 25.4˚

The velocity is: 8.8m/s @ 25.4˚

b) tan(25.4˚) = x/40m
To solve: (40m)(tan25.4˚) = x
x = 19m

c) v = d/t therefore t = d/v
t = (40m)/(8m/s)
t = 5s

Problem 2
A river flows due south. A riverboat heads 27˚ north of west and is able to
go straight across the river at 6 mi/hr. (see diagram below)
a) What is the speed of the current?
b) How wide is the river if it takes 10 minutes to cross?

a) TOA
tan(27˚) = x/(6mi/hr)
(6mi/hr)(tan27˚) = x
3mi/hr = x

b)v = d/t therefore d = vt
You cannot mix different units so minutes have to be converted into hours: 10min = .08hr
(6mi/hr)(.08hr) = 1hr

Examples of how river vectors are applied in the real world:

River Vectors worksheet 1
River Vectors worksheet 2
River Vectors worksheet 3
River Vectors Homework 1
River Vectors Homework 2