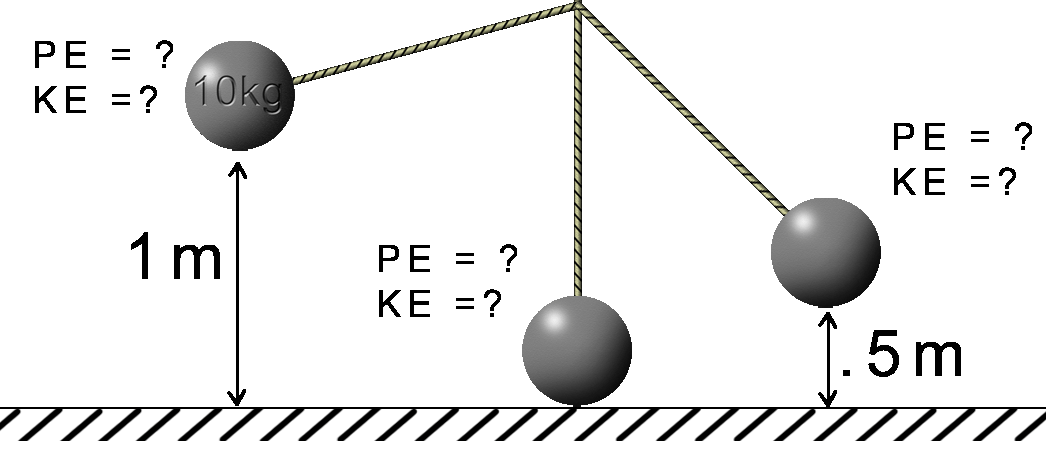Work
Work = ΔE =F•d
Units are N•m or J (Joules)
Work is a change of an object’s Energy (ΔE)
Acceleration changes KE (½mv2)
Lifting changes PE (mgh) |
For work to be done, the force must be in the same direction as the movement.
How much work is done?
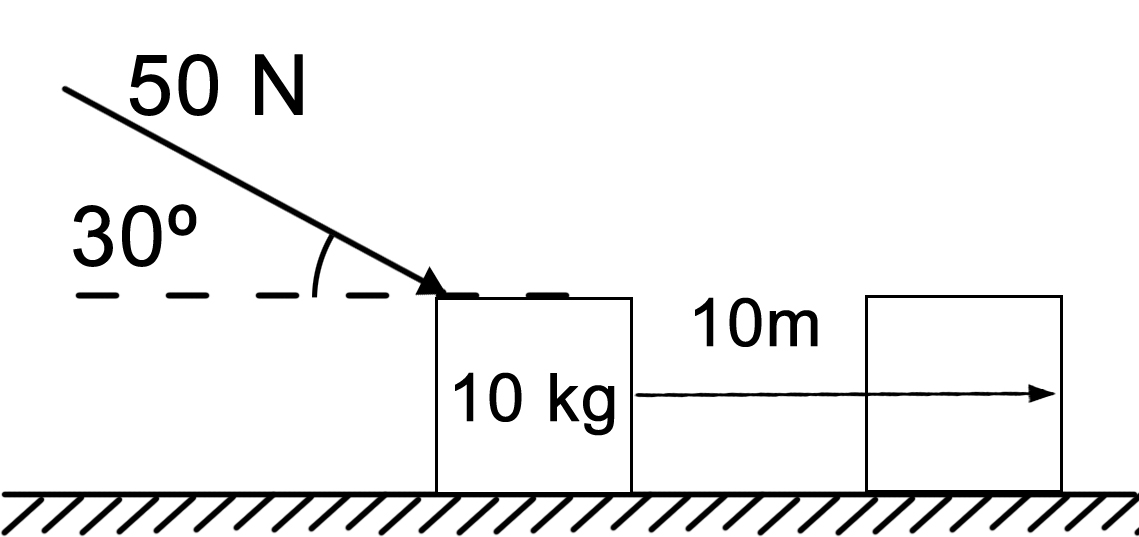
(50N)(cos30˚) = 43.3N
W = F•d = (43.3N)(10m) = 433N•m
433J
Work:
Lifting a box to shelf
Pushing a car
A waterfall turning a water wheel
Not work:
Pushing on a wall- really really really hard! (d=0m)
Carrying a box 10m (Force is at right angles to movement)
Gravity pulling a satellite into a circular path (Force is at right angles to movement) |
Forms of Energy
-
Chemical- stored within the bonds between atoms and molecules.
- Examples would be burning, exploding, electricity from batteries.
-
Nuclear- the energy stored within each atom. This energy will be released when atoms are annihilated or the particles are changed into other types of particles.
-
Internal- the energy associated with the random, disordered motion of molecules.
-
Potential- stored energy
-
Kinetic- energy of movement
-
Q: any other form of diffuse energy (heat, sound, light)
Units of Energy: Joules (J)
1 J = kg•m2/s2 or kg•m/s2•m
Or N•m
(or Pa•m3 or W•s) |

Named after James Prescott Joule
December 24, 1818 – 11 October 1889
Was an English physicist and brewer.
(Quite a combination!)
Potential Energy
Potential energy is stored energy.
It can be stored in the height of an object, which will then have the ability to fall.
It can be stored in a spring about to push or pull.
P.E.g = mgΔh
P.E.s = ½kx2 (potential of a spring)
Where:
k = spring constant: how hard it is to stretch
x = distance stretched
More on springs later.
Kinetic Energy
K.E. = ½mv2
More velocity = more energy |

(Disclaimer: I didn't take the picture.
The car and boy are parked on the side of the road.
It is photoshopped with a motion blur to look like moving.
When these speed signs malfunction, they read 99 all the time.
Professional driver on a closed course )
Work = ΔETotal = ΔK.E. + ΔP.E + ΔQ
Again: Work is a change in an object's energy (ΔETotal)
If any numbers do not add up, it will be due to any energy lost to Q. Q is any type of waste energy that bleeds the energy out of the system. It will be lost through friction, sound and light and will ultimately turn into heat.
Gravitational Potential Energy (PEg)is energy stored in the height that an object can fall. If you use force to push an object to a height, when it falls, it will release the energy. A more practical description is to measure the height that it will change while falling.
Consider this:
You are on the second floor of a building, you climb up a chair, then stand on a desk, then lift a ball can prepare to drop it. How much potential energy will it have?
Depends!
It can fall onto the desk.
It can fall onto the chair.
It can fall down to the floor.
It can fall down through the floor to the first floor.
It can fall right through the building and through the Earth until it reaches the core of the planet and literally has zero height.
Well! Which is it?
The best way to measure PEg is to calculate it with how far it will fall in this situation (Δh) It will become tedious to constantly adjust your height to be from sea level. All that is really needed is the change in height that the object will experience. |
The typical type of exercise involving PEg is when it converts into KE as the object falls and speeds up.
The most classic example is a roller coaster. At the top it has its maximum potential energy. As it drops, the PE converts to the KE of the speed of the coaster. At the bottom, it will not be able to fall any further so all the energy will be locked up in the KE of movement. However, as it climbs up the next hump using its own speed to do so, the train will slow down, losing KE but will gain height. This can go on forever but Q keeps bleeding off a little energy through friction, sound and vibration.
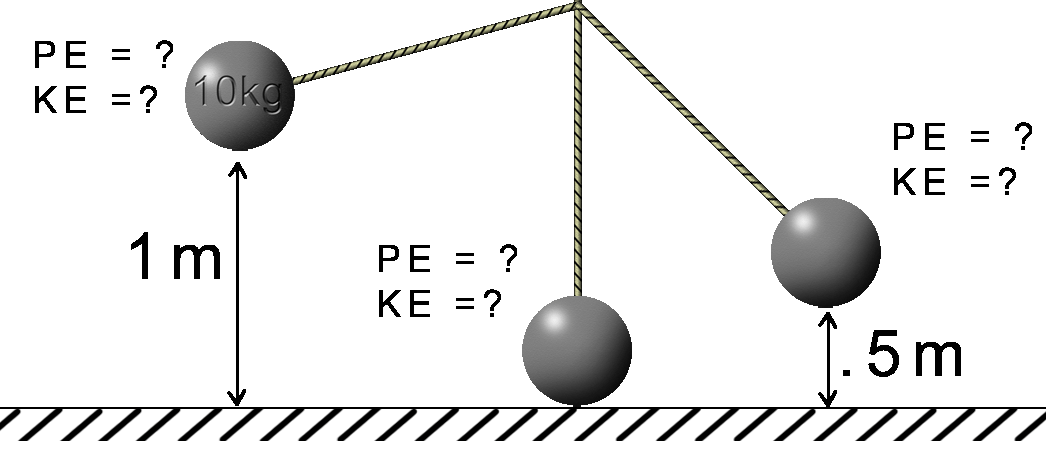
Left:
PE = mgh
= (10kg)(10m/s2)(1m)
=10kg•m2/s2
=10J
KE = ½mv2
KE = (.5)(10kg)(10m/s2)(0m/s)
= 0J
ETotal = 10J |
Middle:
PE = mgh
= (10kg)(10m/s2)(0m)
=0kg•m2/s2
=0J
KE = 10J
ETotal = 10J |
Right:
PE = mgh
= (10kg)(10m/s2)(.5m)
=5kg•m2/s2
=5J
KE = 5J
ETotal = 10J |
Note: These calculations were done the easy way by assuming that any energy lost by PE was automatically gained in full by KE. However, by employing the equations of movement, the actual velocity can be calculated and thus, the KE.
If KE is assumed to be whatever energy PE is missing due to the loss of height, then the velocity can be calculated by using the KE equation and solving for v
v = √2KE/m
|
Potential Energy of a Spring
PEs = ½kx2
k = spring constant (strength of the spring)
Units N/m
x = elongation (distance stretched)
Hooke’s Law:
Fs = kx
|
Work = ΔETotal = Δ K.E. + Δ P.E. (mgh and/or ½kx2) + Δ Q
The Spring Constant
k is the strength of the spring. It is the Force needed to stretch the spring so many meters long.
Units for the spring constant: N/m
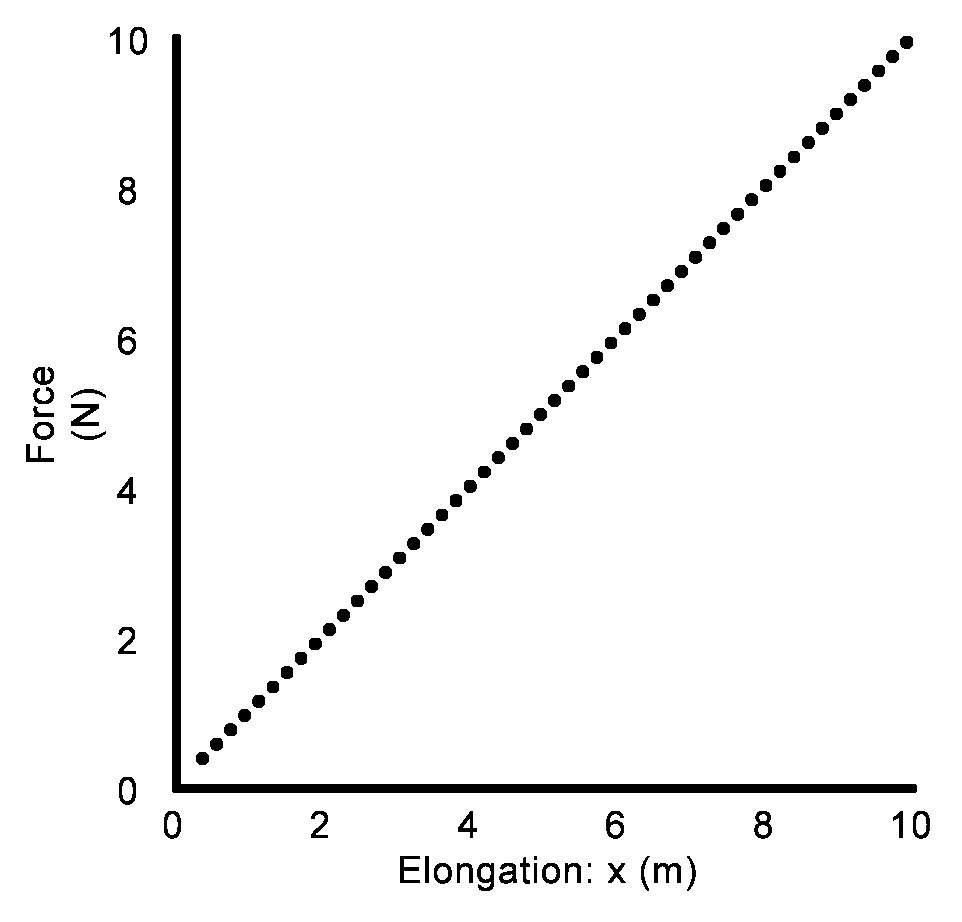
k = slope of the line on an F vs d graph
k = slope Δy/Δx = ΔF/Δd = F/x = 10N/10m = 1N/m
Alphabet Soup:
At this point we have a lot of equations swirling around. Let's put them all in one place:
Work = ΔETotal = ΔK.E. + ΔP.E + ΔQ
Work = F•d = Δ½mv2 = Δmgh = Δ½ kx2
Power (Watts) = Work/t
J = N•m = kg•m2/s2 = (kg•m/s2)(m)
N = kg•m/s2
J = kg•m2/s2
Watt = J/s |
Finding Work graphically
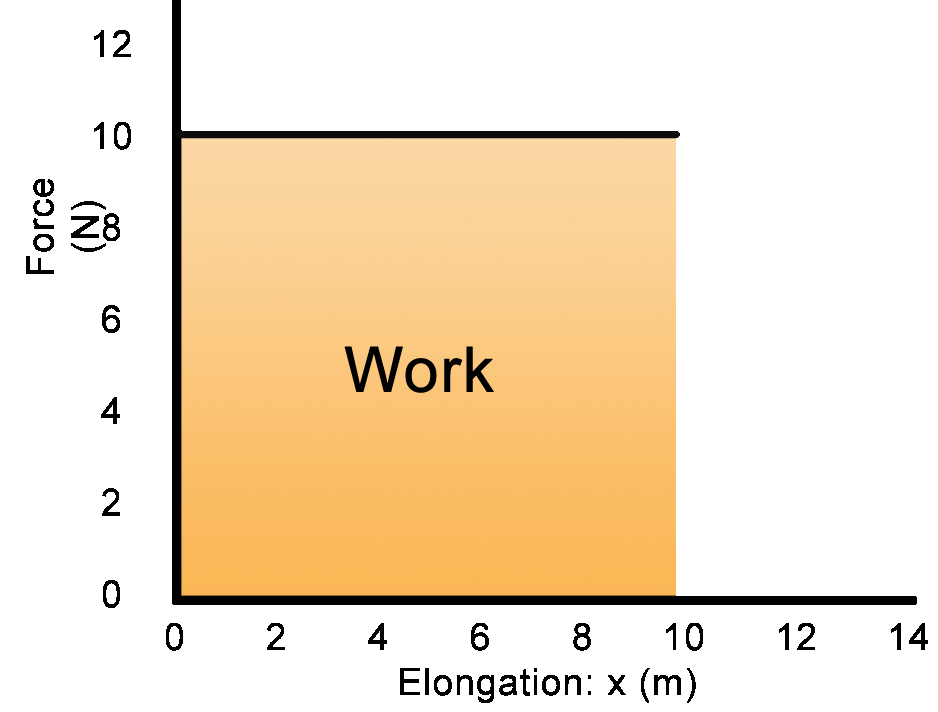
W = F•d
10N x 1m = 10J
10N x 2m = 20J
10N x 3m = 30J
10N x 4m = 40J
...
10N x 10m = 100J
Work is the area under thecurve |
With a varying force such as a spring:
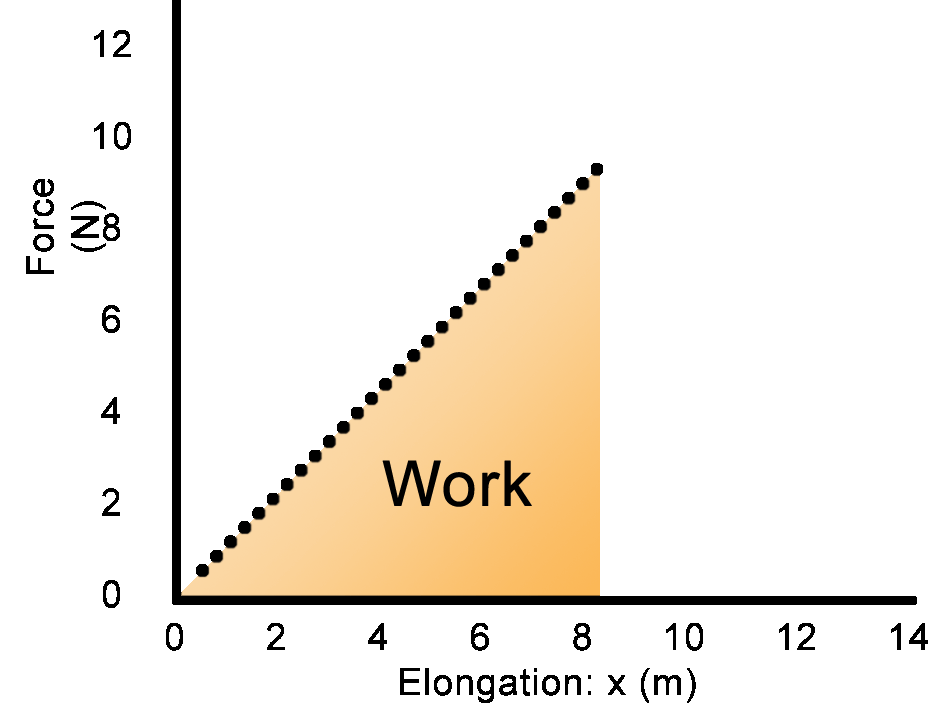
W = F•d
W = Area under curve
W = (½b•h) = ½F•x (Area of the rectangle then cut in half)
Riddle me this:
You are a twerp.
Your friend is an ox.
You both have to move a ton of bricks from the floor up to the counter.
You both accomplish the task.
You both moved the same weight the same distance.
Therefore you both accomplish the same amount of work.
So what’s the difference?
The difference is how quickly each of you was able to accomplish the same job.
Which brings us to...
Power:
How fast you can do work
Power = work/time
Rate at which energy gets used or rate at which work is done.
Work/time = J/sec = Watt (insert hard-of-hearing joke here)
1HP = 746W
More Alphabet Soup:
Power = W/t = F•d/t = F(d/t) =F•v |