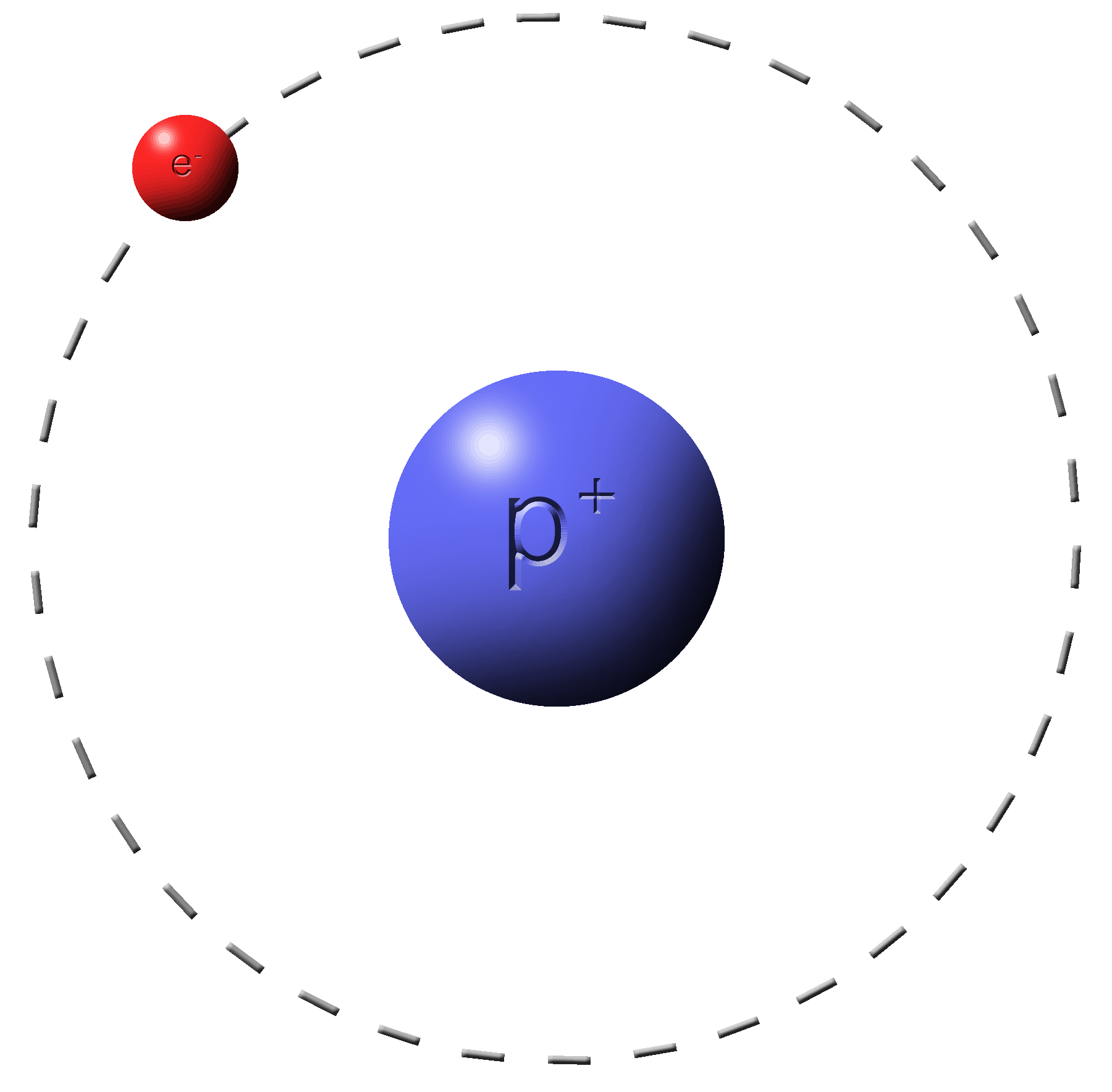
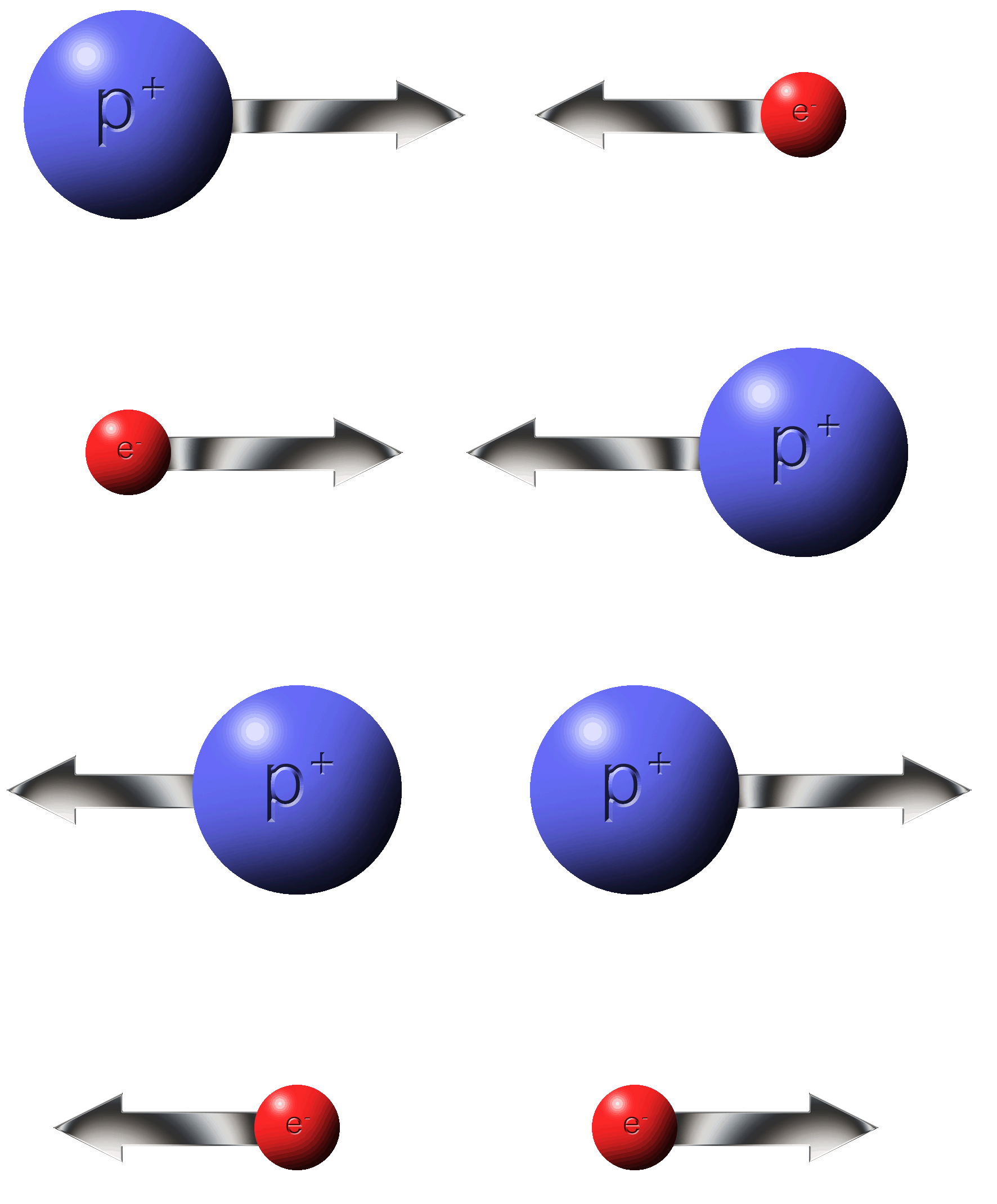
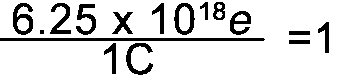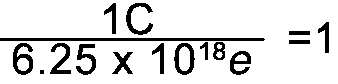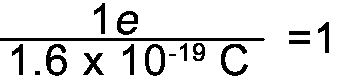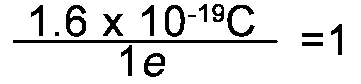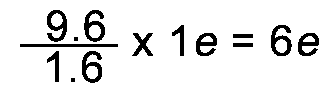Rule #2:�Electrons do the moving.�Protons do not.
You can’t touch this!
- An electron cloud surrounds atoms.
- Electrons do not like each other.
- When you bring your hand near an object, the electrons begin to repel each other.
- You feel this repulsion as pressure against your skin… touch.
- Yet you never actually touched the object.
- Freaky!
|
In a solid material: (Which is what we are dealing with here.)
Protons are stuck where they are.
Electrons are more free to move around.
Some materials allow electrons to move easily, others, not so much.
Some materials like to absorb electrons,
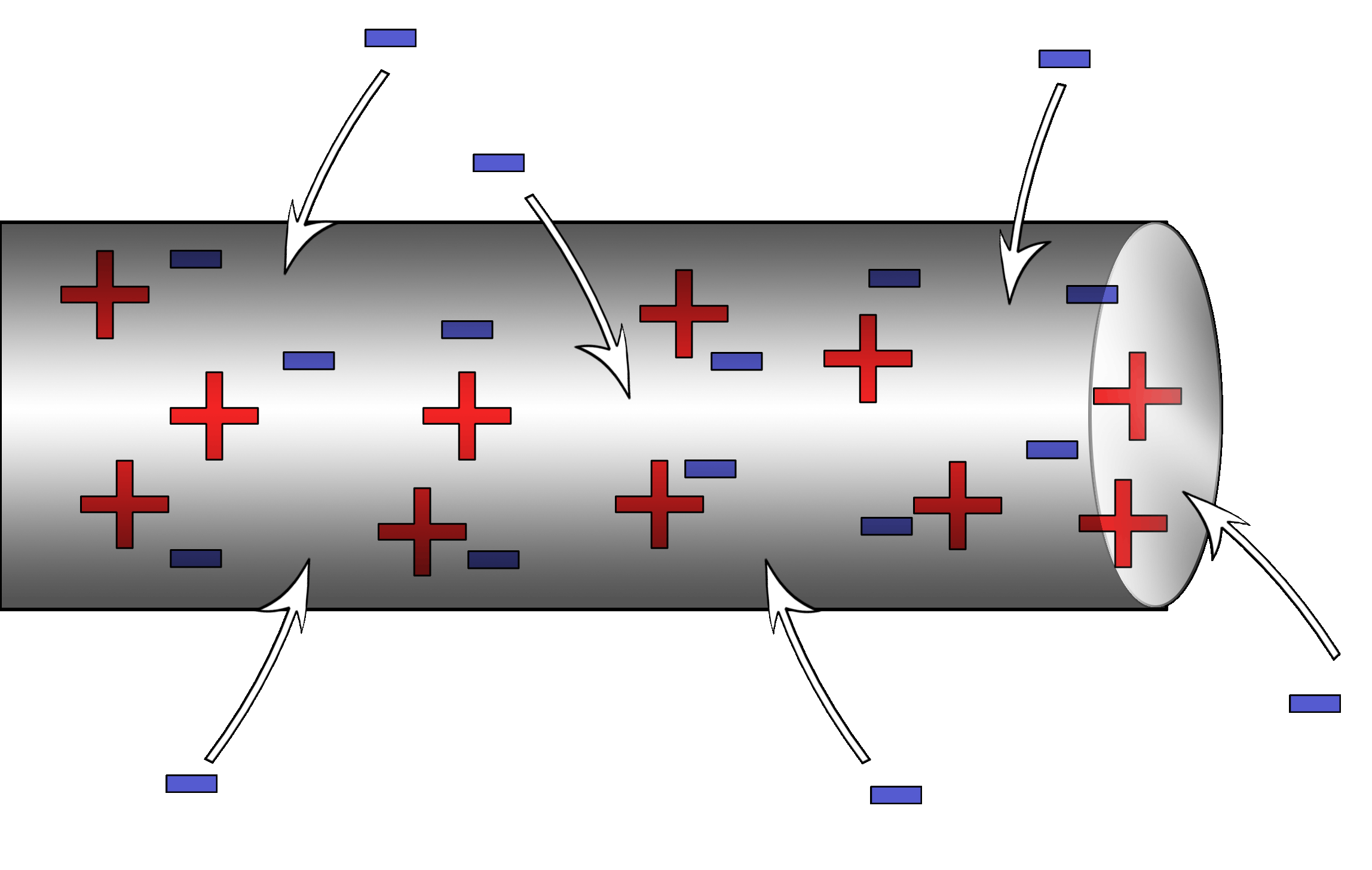
they become more negative.
Other materials push electrons out,
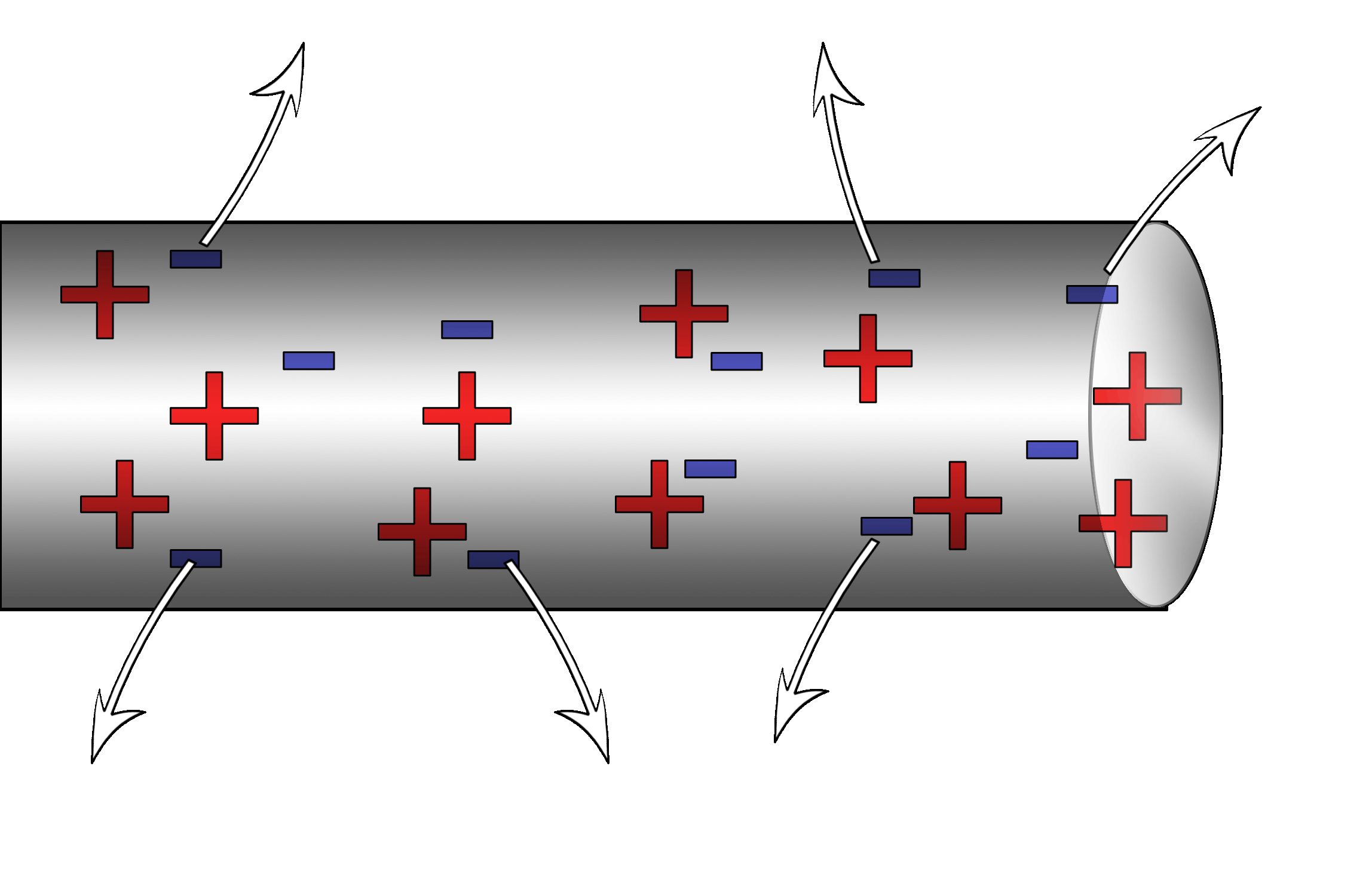
they become less negative (positive).
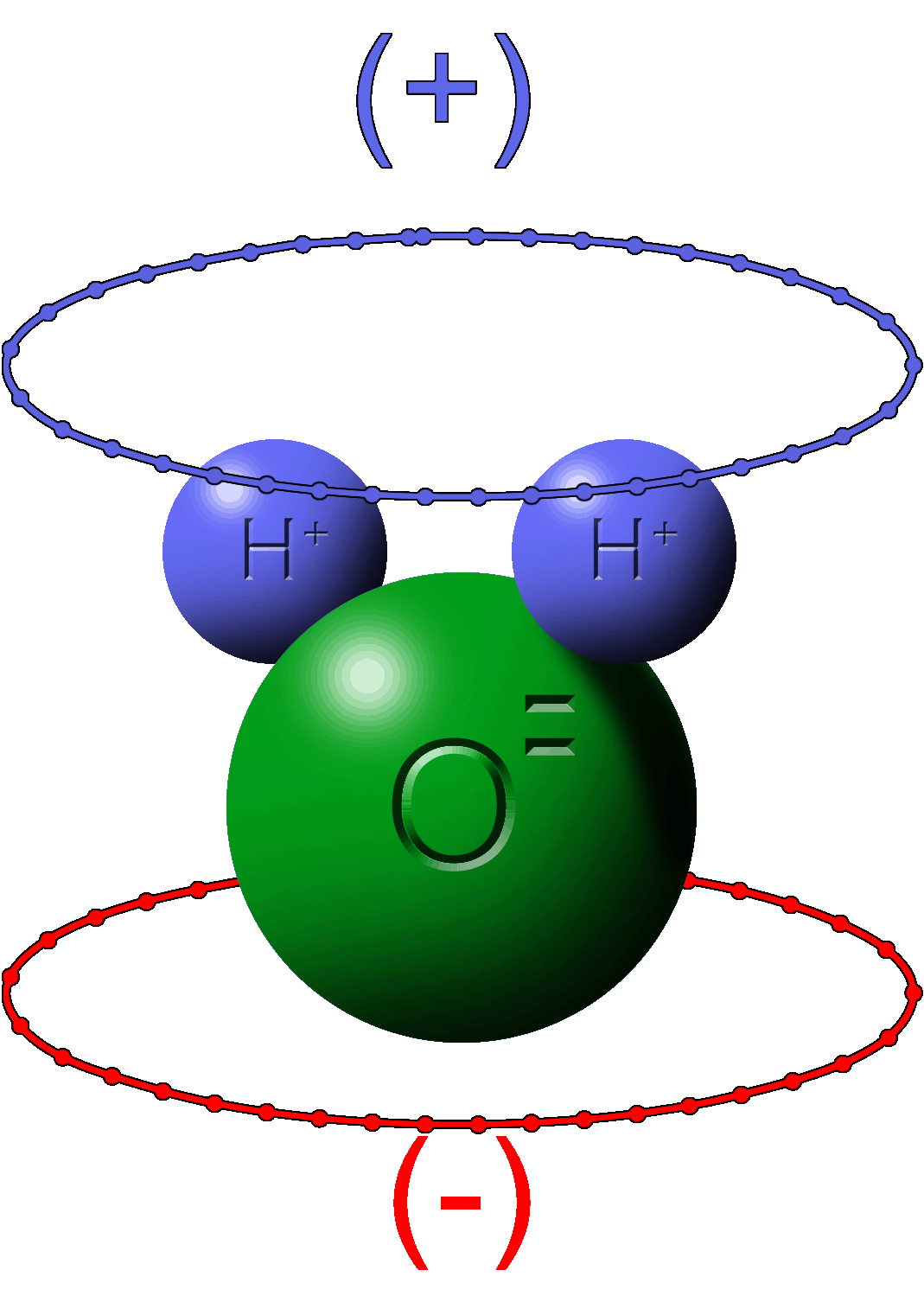
Yet, other materials are neutral but rearrange the electrons to give the illusion of a net charge. This is polarity.
Neutral water has a positive side where electrons have vacated and a negative side where the electrons have gathered.
|
 |
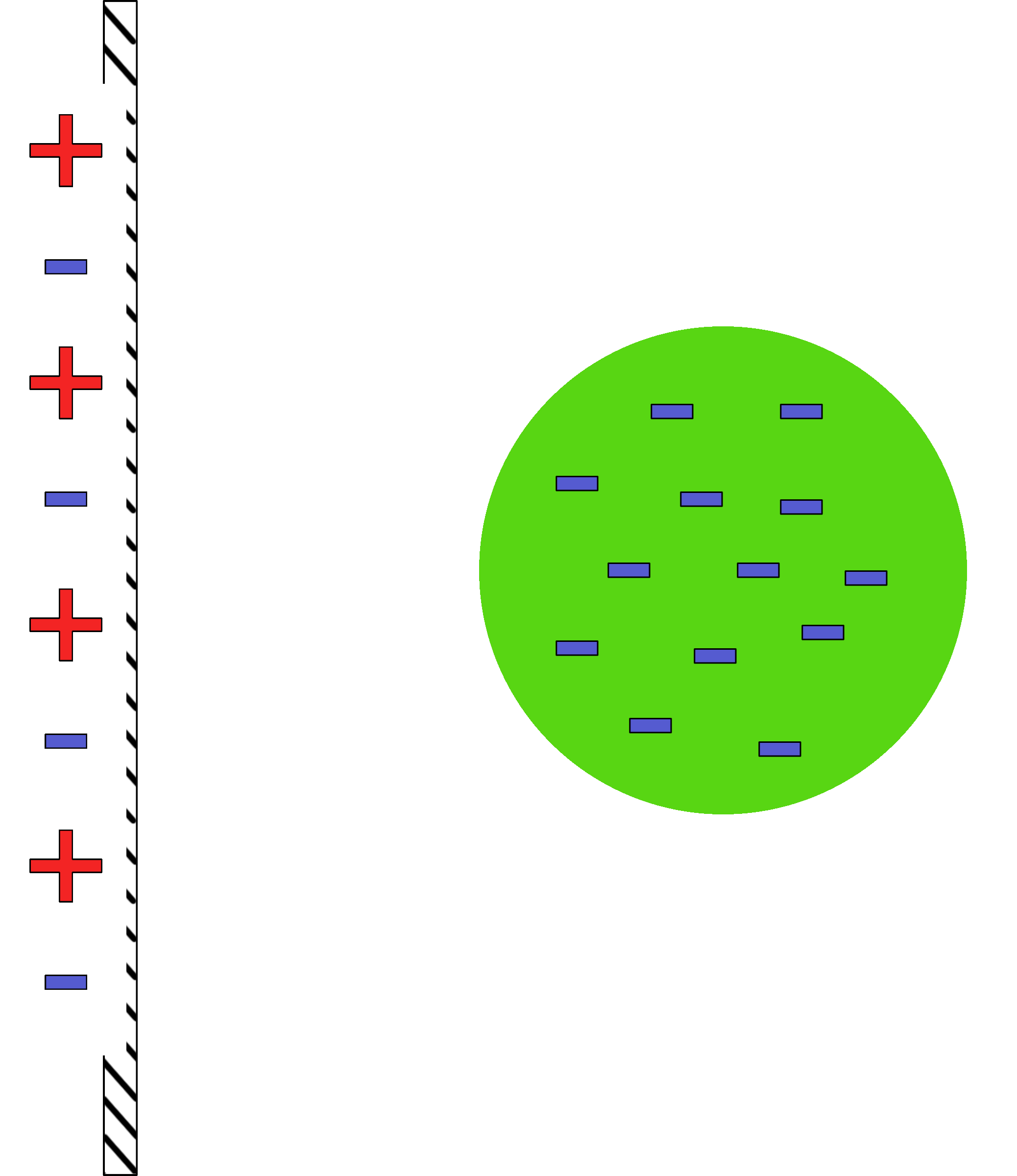
Induced Charge Separation
Charges are rearranged based on an introduced charge.
Before getting close |
After getting close |
|
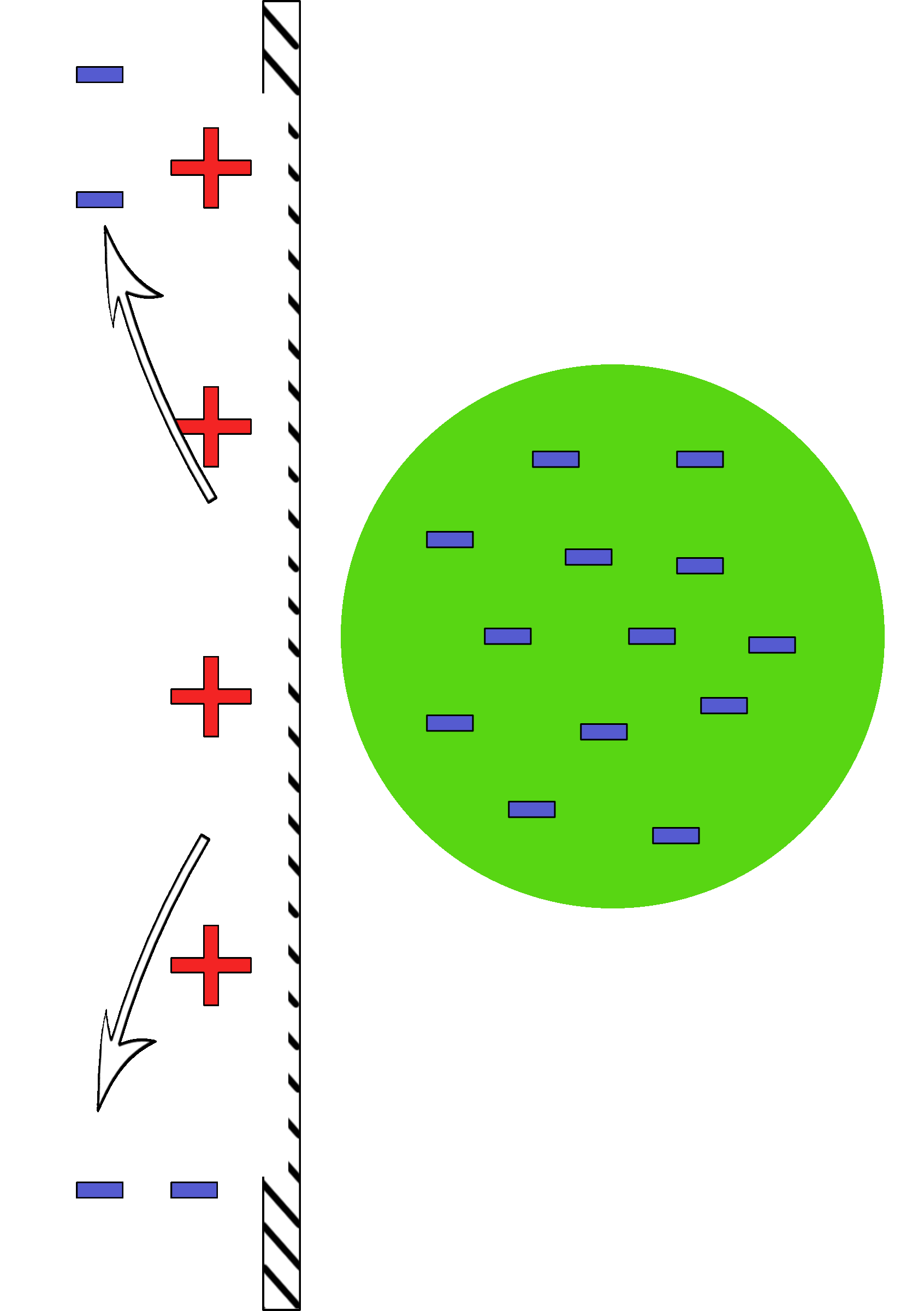 |
A negatively charged ball is brought near a neutral wall.
|
As it nears, the electrons in the ball push the electrons in the wall away. This leaves behind the protons which give an attractive positive area. |
“Pith Ball” is a small light ball made of light-weight wood, plastic, or foam and is often covered with a thin layer of metal. The ball hangs from a non-conducting thread. Originally the ball was made from a plant called pith. |
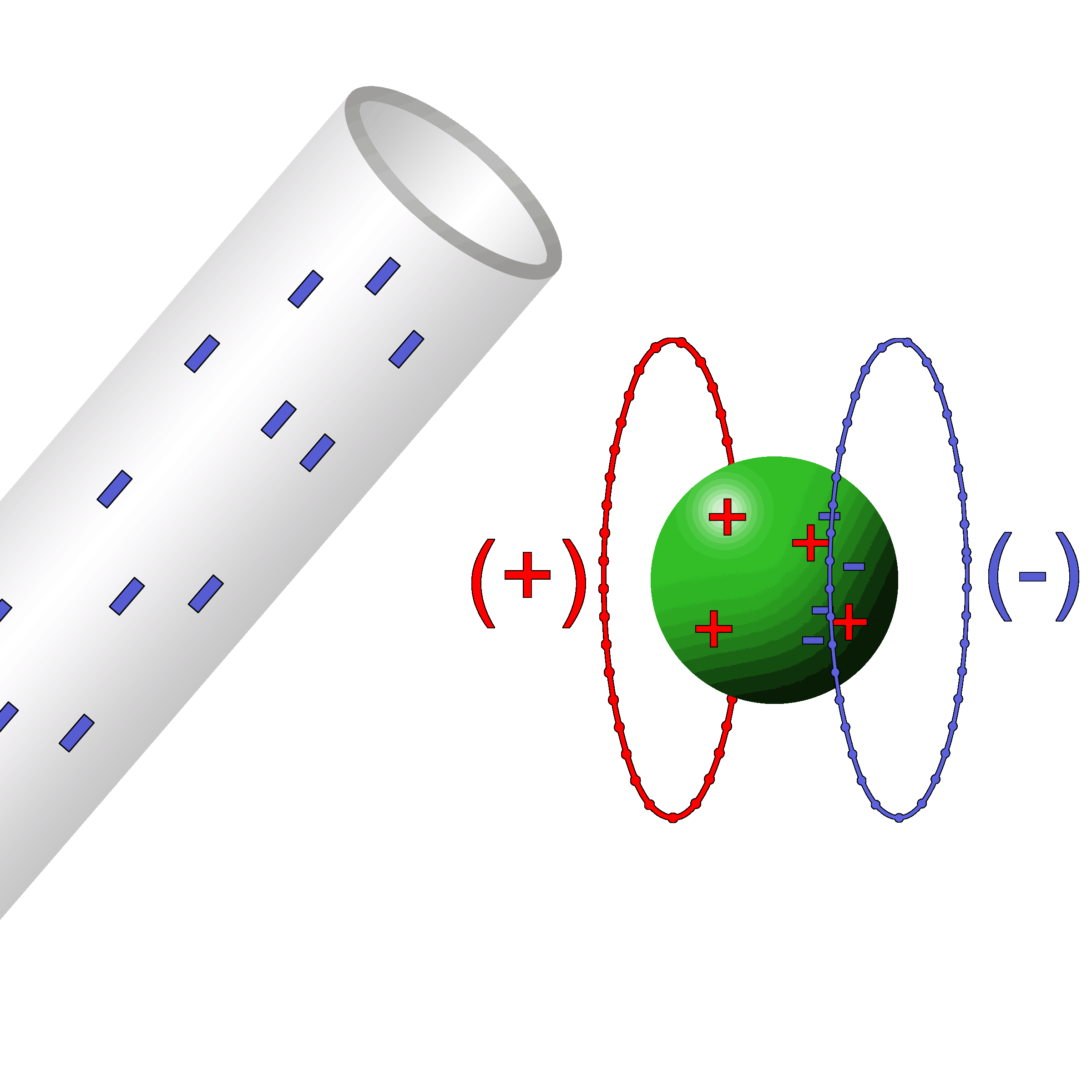 |
When a negatively charged rod is brought close to a neutral pith ball the electrons in the ball are chased away to the other side. The positive charges remain behind on the near side creating an attraction to the charged rod. |
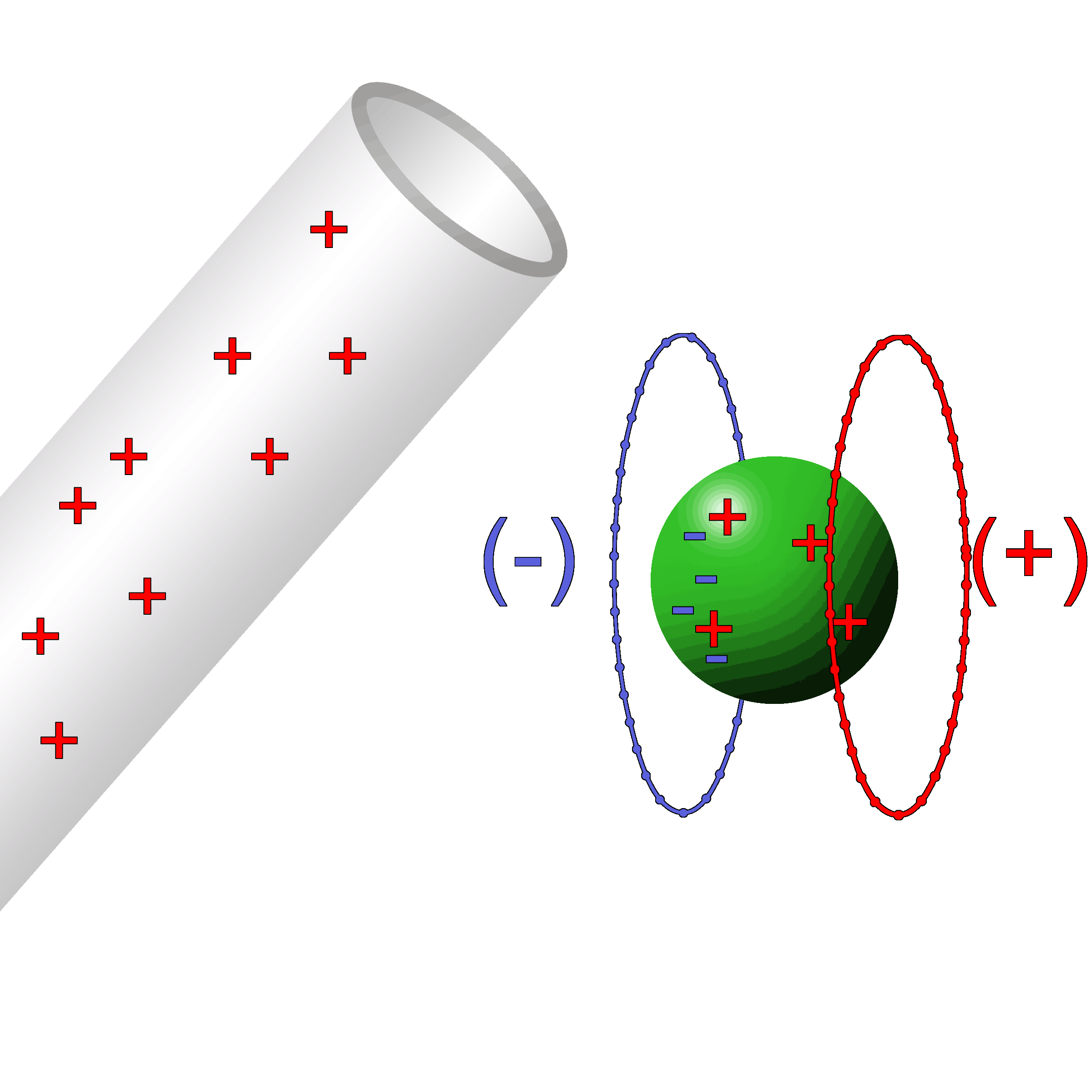
When a positively charged rod is brought towards the pith ball, the electrons are attracted to the rod and the ball is carried closer to the rod. |
 |
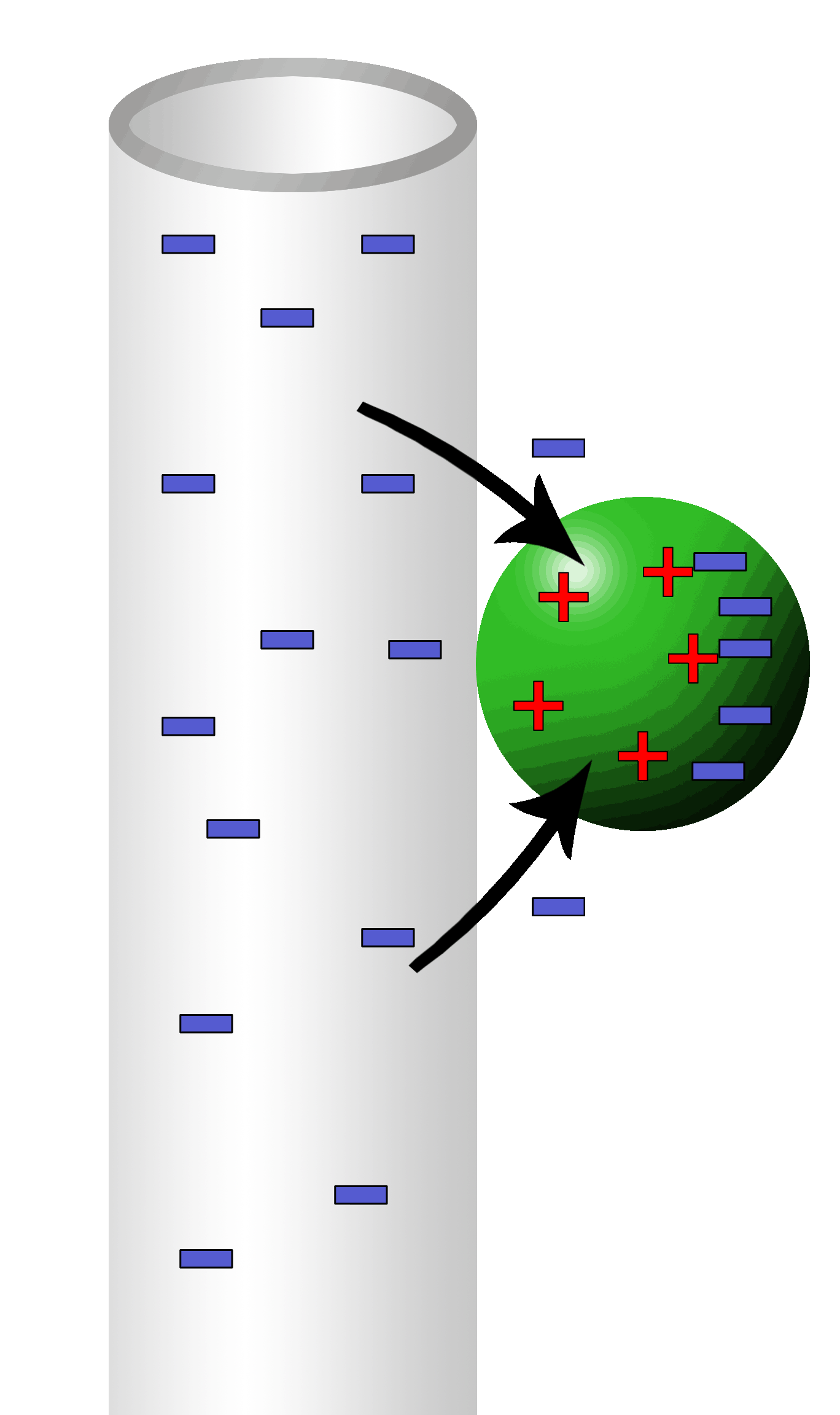 |
When the two come in contact with each other, electrons will jump. In this case, the highly concentrated electrons of the rod will repel each other and force some out of the rod. The pith ball will draw in the electrons since the near side of the ball is mainly protons. After the jump, the ball now has a surplus of electrons. It is no longer neutral, it is now negatively charged. The negative rod and negative ball repel each other and suddenly fly apart. |
How strong is the force supplied by the electrons?
We now see that the attraction and repulsion of the charges produces a force. This is Physics so of course we have an equation to calculate the strength of the force. But first, some definitions:
Charge (symbolized with a q “quantity of charge”). There are two main measures of charge: |
Coulomb (C)
- a large collection of electrons
- think of it as a crate of electrons
- 1C has 6.25 x 1018e (see right side)
|
Elementary Charge (e)
- this is the most basic charge there can be
- has the value of a single electron (or proton since they have equal but opposite charges shown as + or -)
- technically, the symbol e stands for “elementary charge” since it can represent either a proton or electron but it is easy to connect e with electron.
- 1e is 1.6 x 10-19C
|
It doesn’t look like it but 6.25 x 1018and 1.6 x 10-19 are inverses of each other. Really! Take 1 and divide it by 1.6 x 10-19 and you will get 6.25 x 1018. More on working with these later. |
Coulomb's Law:
Calculates the strength of the electric force.
Fe = kq1q2/r2
- q = the charge involved. Can be either e or C
- k = the electrostatic constant
- this adjusts the value of the equation so that the numbers reflect what is observed
- 8.99 x 109N•m2/C2
- r = the distance (radius) between the charges
You’ll notice that this equation looks very similar to Newton’s Law on Universal Gravitation. That’s because the two forces work in pretty much the same way. They merely have different constants that adjust for the strength of each force. The electric force is much much stronger than gravity. Hence, the positive exponent for electric and the teensie negative exponent for gravity (10-11).
Coulomb simply stole Newton’s equation and changed the letters so that no one would notice. |
What is the force between these two elementary charges?
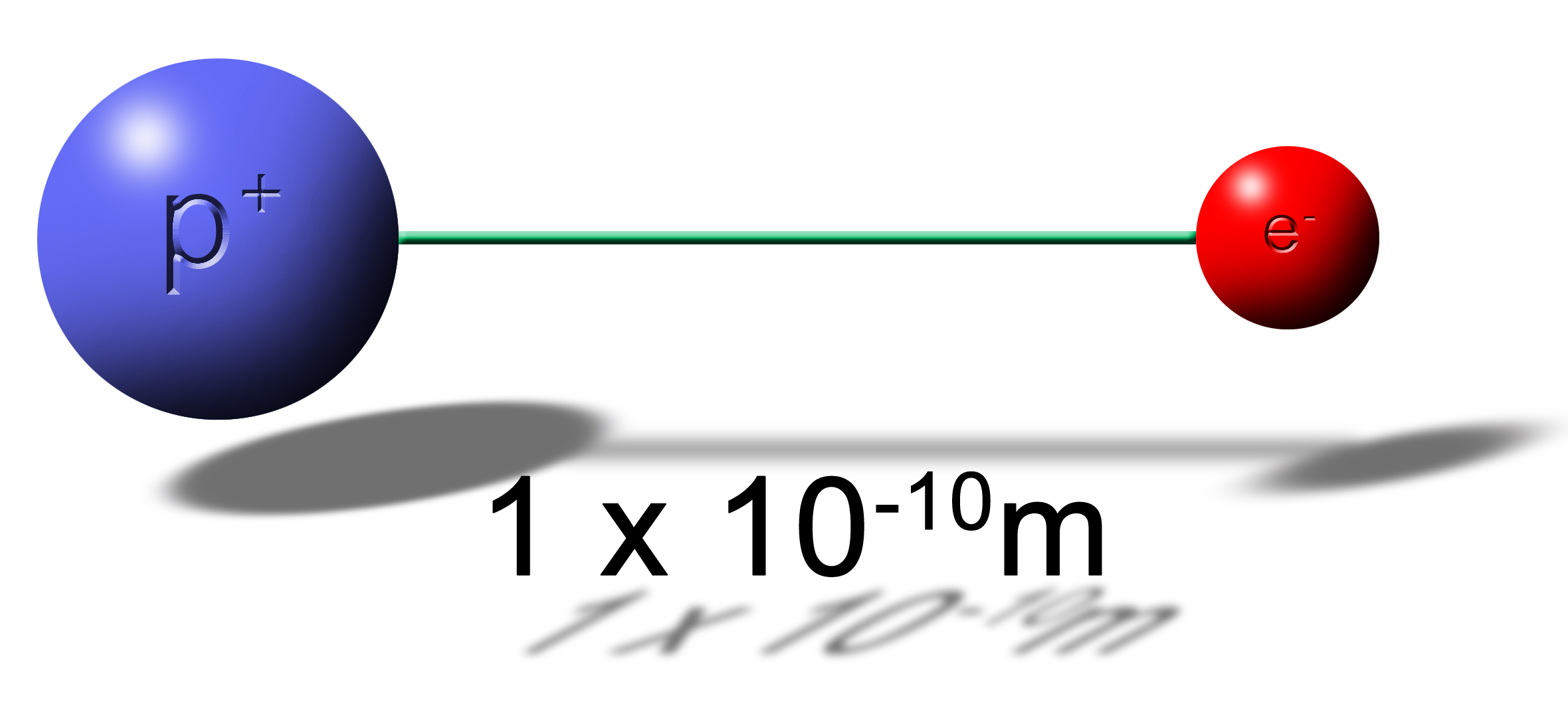
|
| |
Fe = kq1q2/r2
|
With this problem be sure to include the positives (+) and negatives (-) for each elementary charge. This will carry through until the end to tell you if it is an attractive (-) or repulsive (+) force. |
| Fe = |
(8.99 x 109N•m2/C2)(+1.6 x 10-19C)(-1.6 x 10-19C)
(1 x 10-10m)(1 x 10-10m) |
|
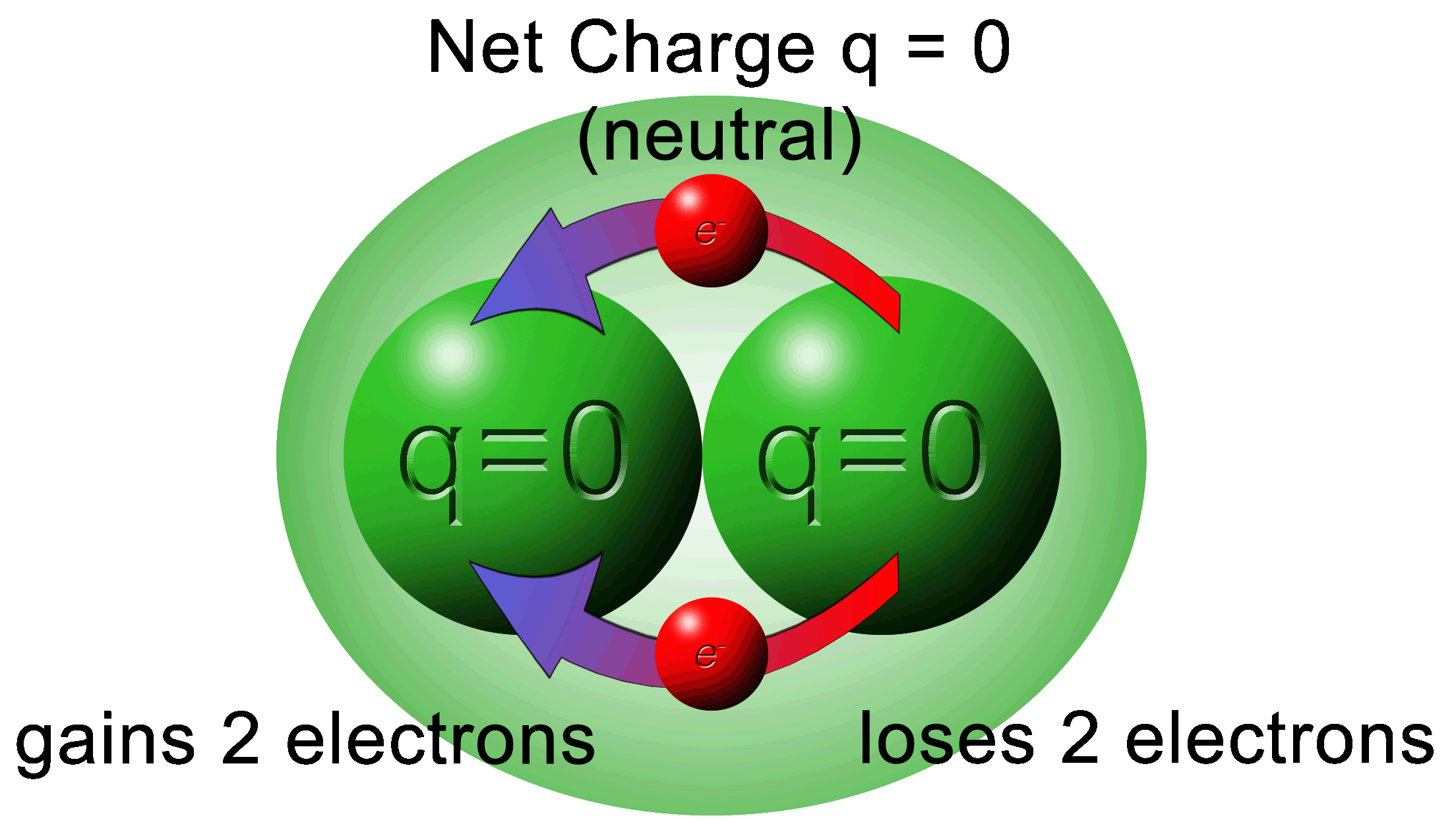
Conservation of Charge
Whatever charge you have at the beginning, you will have at the end.

Overall, the system above made of two charges has a combined charge of zero.
At this point, it looks like there was an error to show +2e but we must remind ourselves that the “e” is elementary charge and not electron. It can be either positive or negative.
Also, we must think of a positive charge as being “less negative” meaning that it has less electrons.
The flow of electrons will always be from the highest amount of electrons (most negative) to the lowest amount of electrons (less negative).
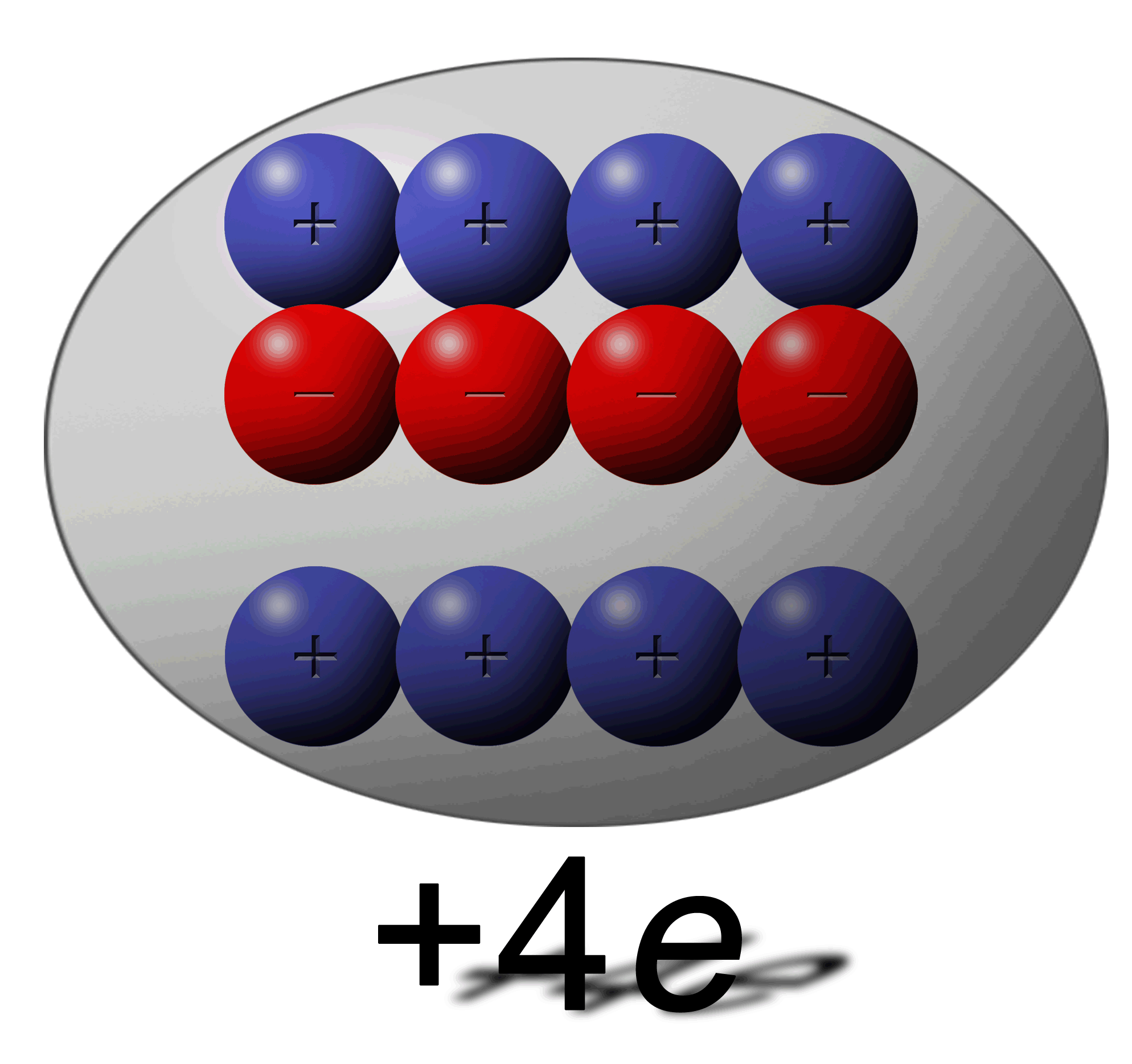
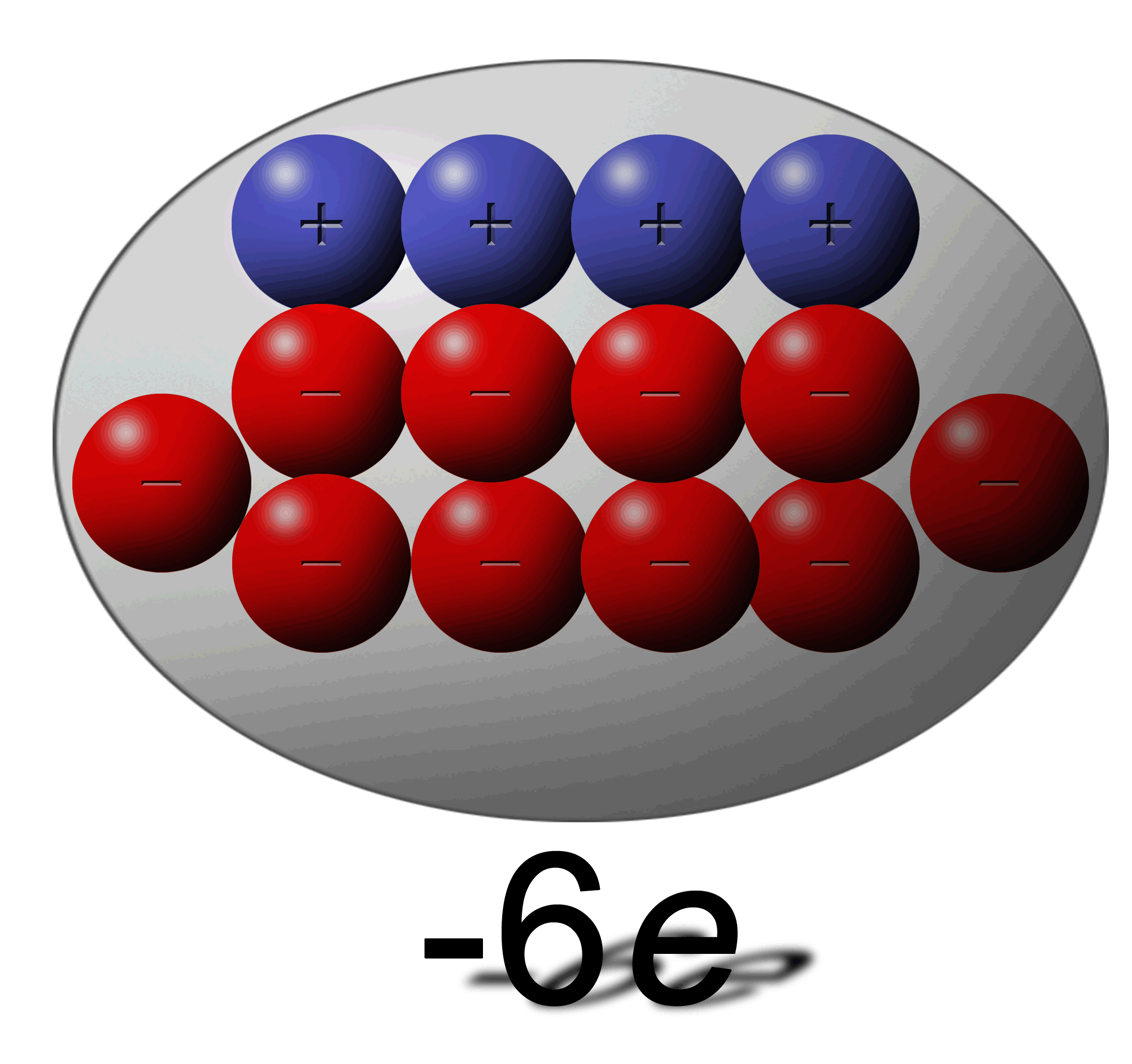
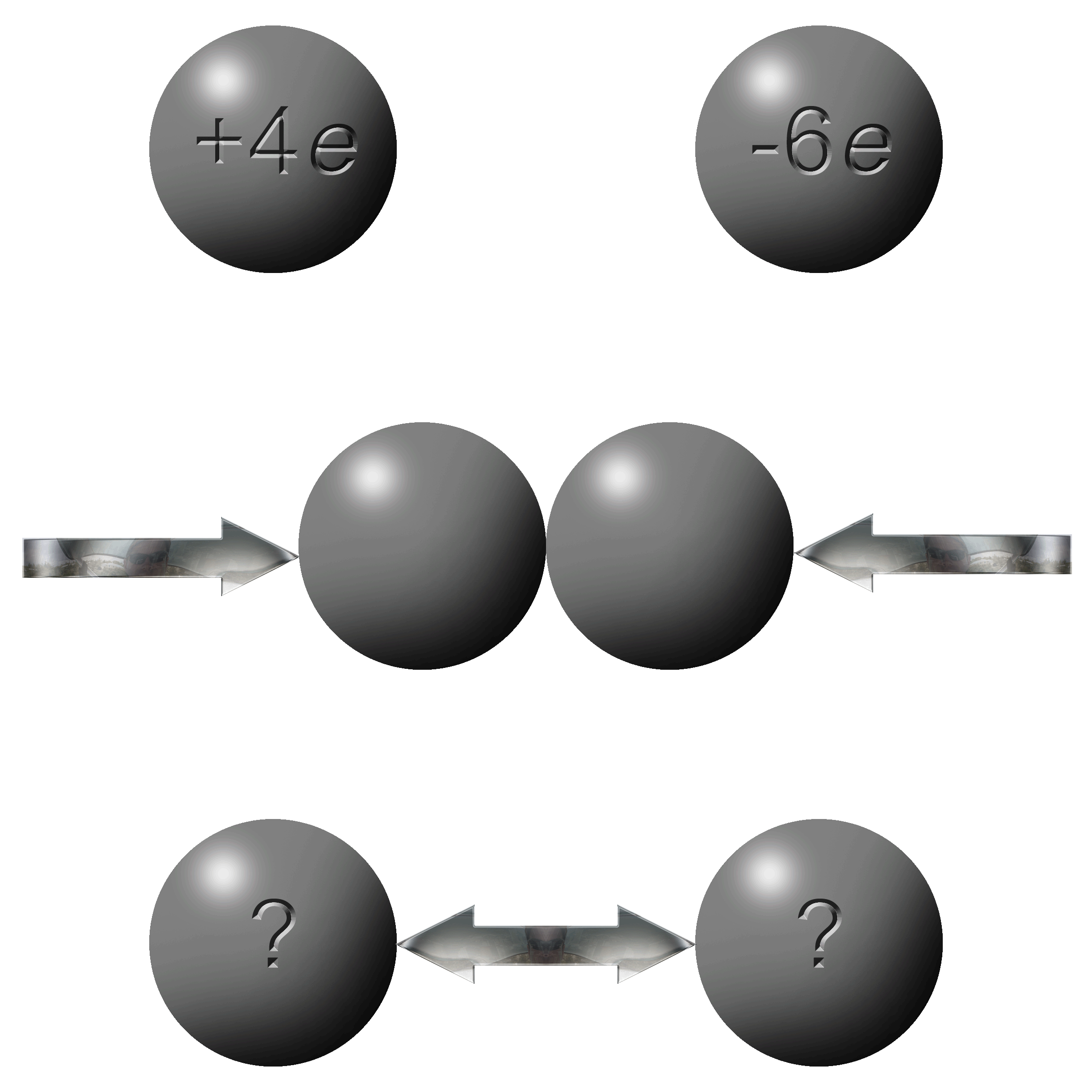
How can this be possible:
You have one sphere with an overall charge of +4e and another with a total charge of -6e? |
|
|
Remember that e stands of “elementary charges” and not necessarily electrons. A +4e charge simply means that it has 4 positive elementary charges more than neutral. In the illustrations above you can see that the +4e charge is missing 4 electrons leaving 4 protons un-neutralized giving a net charge of +4e. |
In the -6e charge it simply has an excess of an extra 6 electrons. A total of ten electrons but 4 of those are negated by the 4 protons. |
 |
Here's the situation: you have two spheres; one with a charge of +4e and the other with a charge of -6e.
They touch. Electrons jump.
Then the two spheres are separated.
What is the charge on each sphere?
|
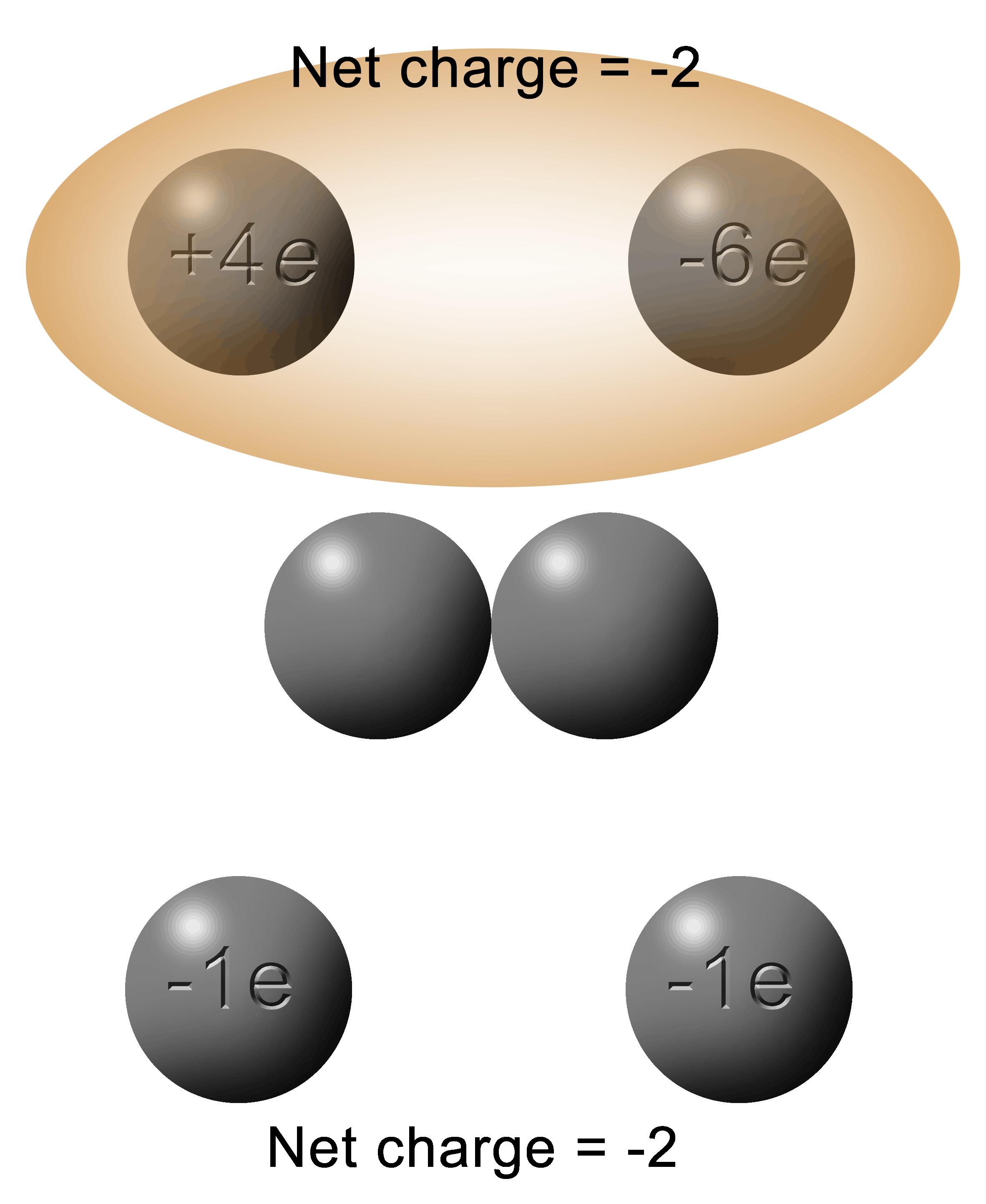 |
The first thing you do is to add up the total charge between the two spheres.
In this case: +4e + (-6e) = (-2)
When in contact, the electrons will flow from the object that is the most negative to the least negative.
Think of it this way: electrons, like most other things, will move from a high concentration where it’s crowded, to areas where it is less concentrated. Electrons repel each other. They will push them away until the other side pushes back just as hard.
That’s how you should think of the electrons moving.
BUT!
To get the solution, you simply add the charges (-2e) and divide it equally between the two spheres (-1e each).
For this situation, the electrons will jump from right to left. |
 |
The total charge here is +14e.
Divide them by 2 and you get +7e on each sphere.
In this case, the electrons move from left to right since the +5e is “more negative” (further left on a number line). |
Riddle: How are electrons like holes? Answer below the next graphic. |
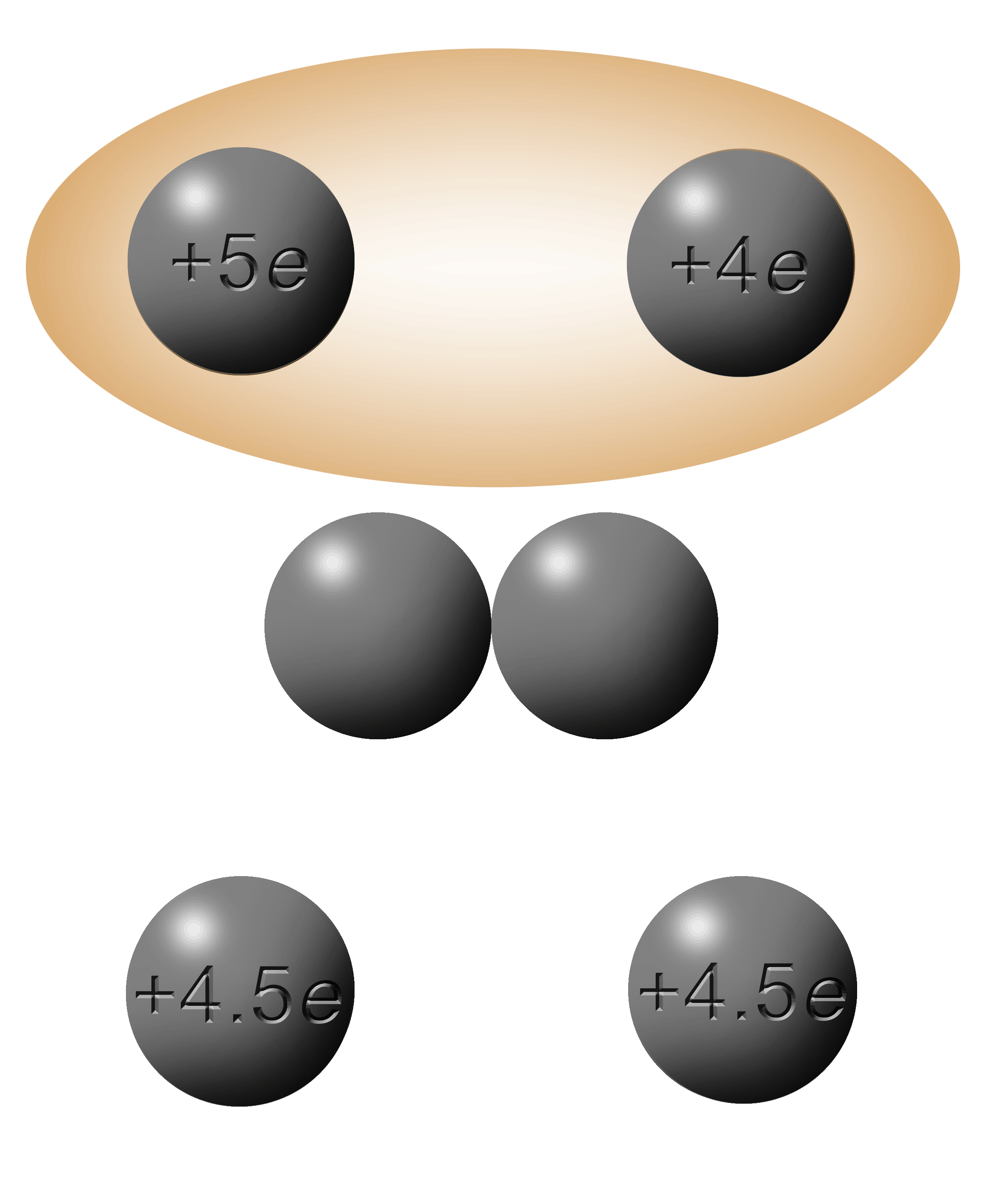 |
This one here presents a problem.
When you add them up and divide by two you end up with -4.5e.
4.5 ELEMENTARY charges
4.5 ELECTRONS
You can’t have half an electron!
(Sorry, didn't mean to yell there but I got excited.)
What would happen in reality would be that the last electron would get pushed back and forth. Whichever side it was on, would have a greater concentration of electrons and one would get pushed to the less negative side, which, in turn will now have the higher concentration. When the two spheres are separated, it will be trapped in whichever sphere it was in at the time.
This one will not work!
|
You can’t have half an electron. You can't have half a hole either. |
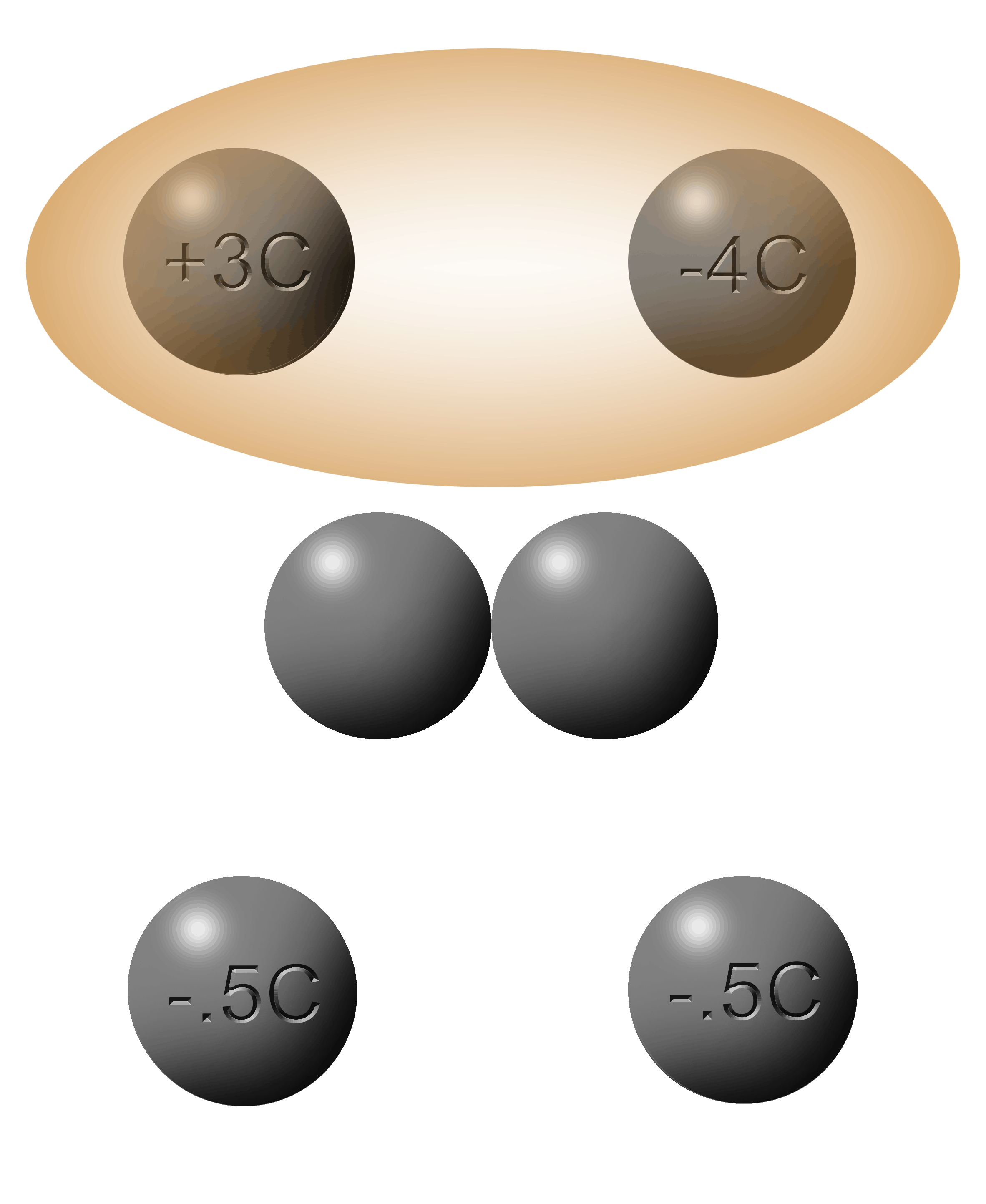 |
The average of these two spheres is -.5C.
Since a Coulomb is a crate of electrons, there are so many that it is easy to get them cut in half.
Coulombs can be cut in half but electrons cannot.
|
Converting from Coulombs to e's
Since 1C = 6.25 x 1018e the following fractions = 1 |
|
|
And since 1e = 1.6 x 10-19C the following fractions also =1 |
|
|
Multiplying by any of those fractions is the same as multiplying by 1.
To convert from C to e or e to C is just a matter of multiplying by whichever fraction that will cause your first unit to cancel out and leave the unit that you want. For each conversion you have two choices. The two examples below have exactly the same result.
Convert 9.6 x 10-19C into elementary charges. |
|
|
|
|
|
|
Both ways of working the conversion gives the same answer of 6e. |
Is it possible to have 5.2 x 10-19C?
When you do the conversion above, the answer will be 3.25e. You cannot have a fraction of an electron (or proton).
Electric Fields
Electric fields work very similarly to gravitational fields, except:
- Gravitational fields are always attractive.
- Ectric fields can be either attractive or repulsive depending on the combination of charges involved
|
|
|
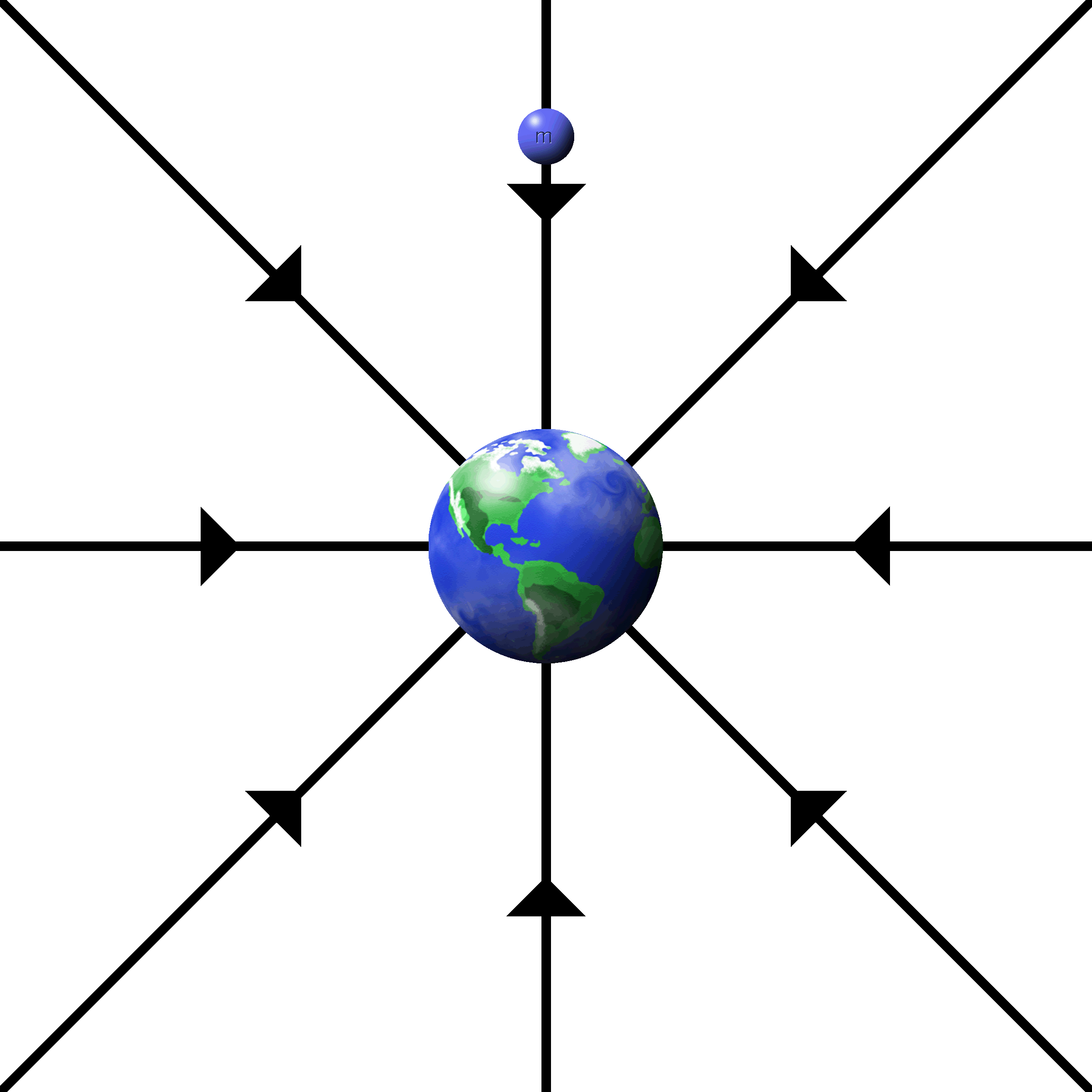
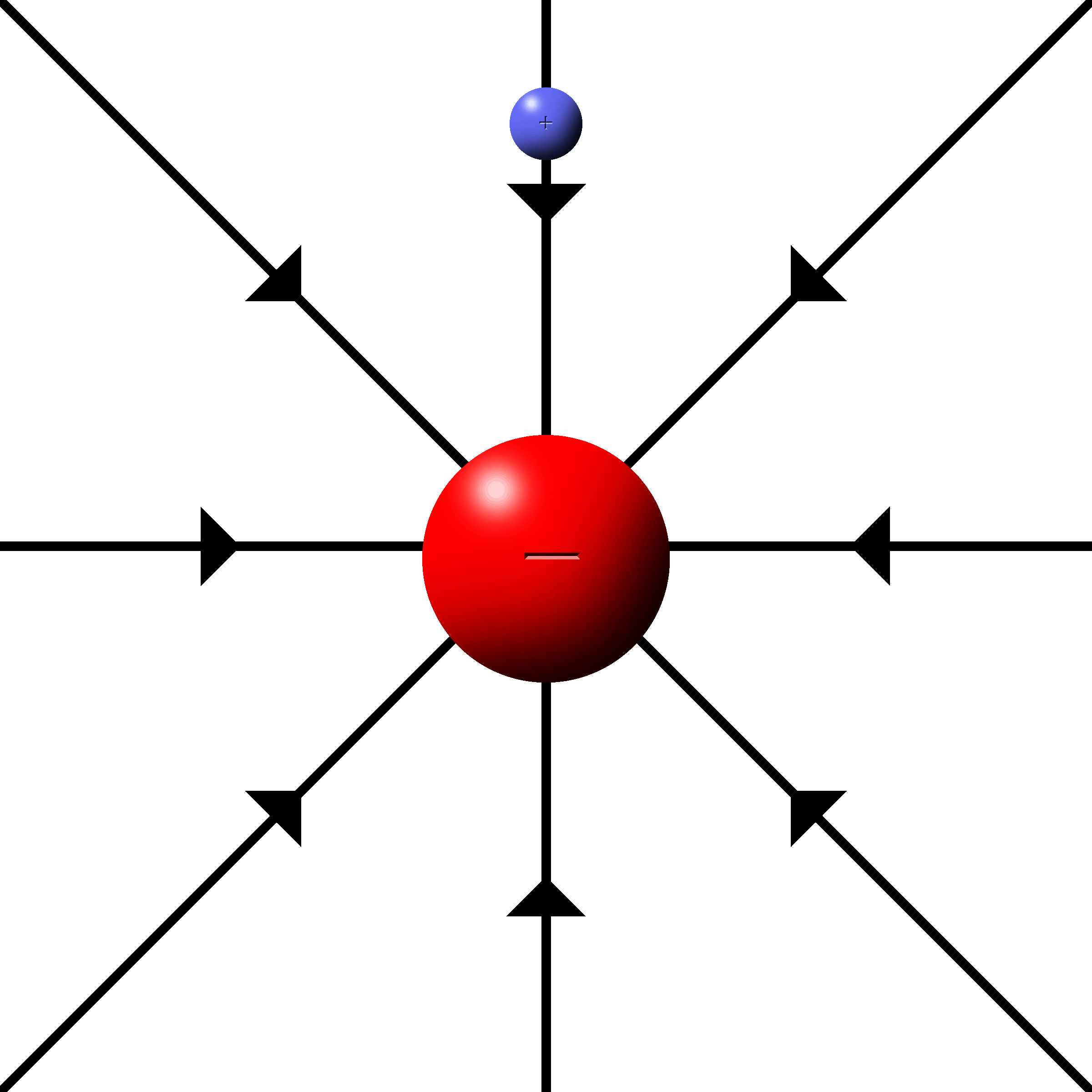
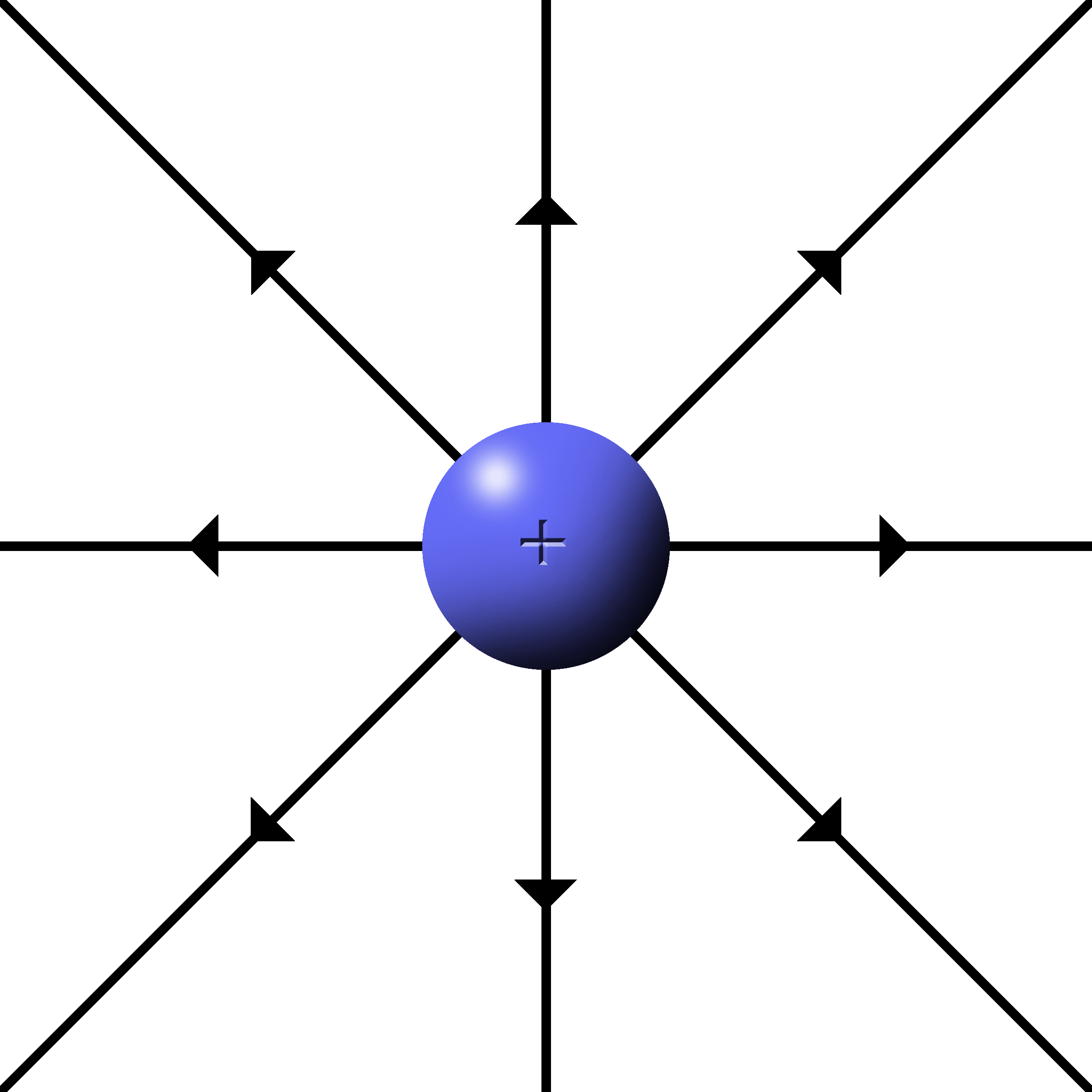
When the fields radiate from a single charge, it is called a point charge.
The fields are drawn as lines starting at the charges that radiate outwards.
The density of lines indicates the strength of the field. More lines, more force.
The push or pull is along the direction of the lines.
(Be sure to have them connect to the charge when drawing them.)
|
Electrons have inward, attractive fields.
|
Protons have outward, repulsive fields. |
 |
 |
What would the field look like if there were two charges in the same area?

Put a test charge in the area.
A test charge is a positive charge that is used to test fields.
|
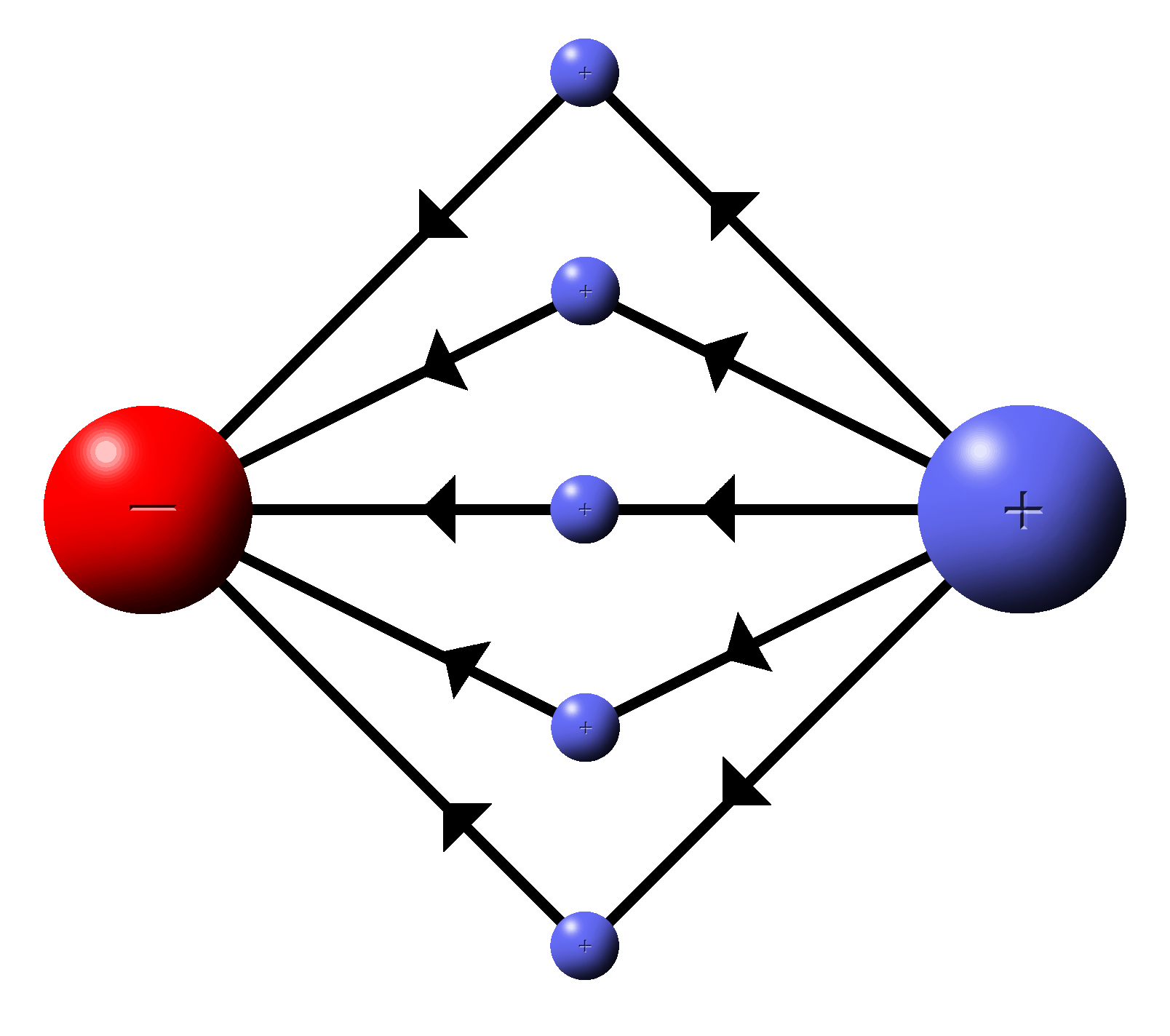 |
The positive test charge will be attracted to the negative charge and repelled by the positive.
|
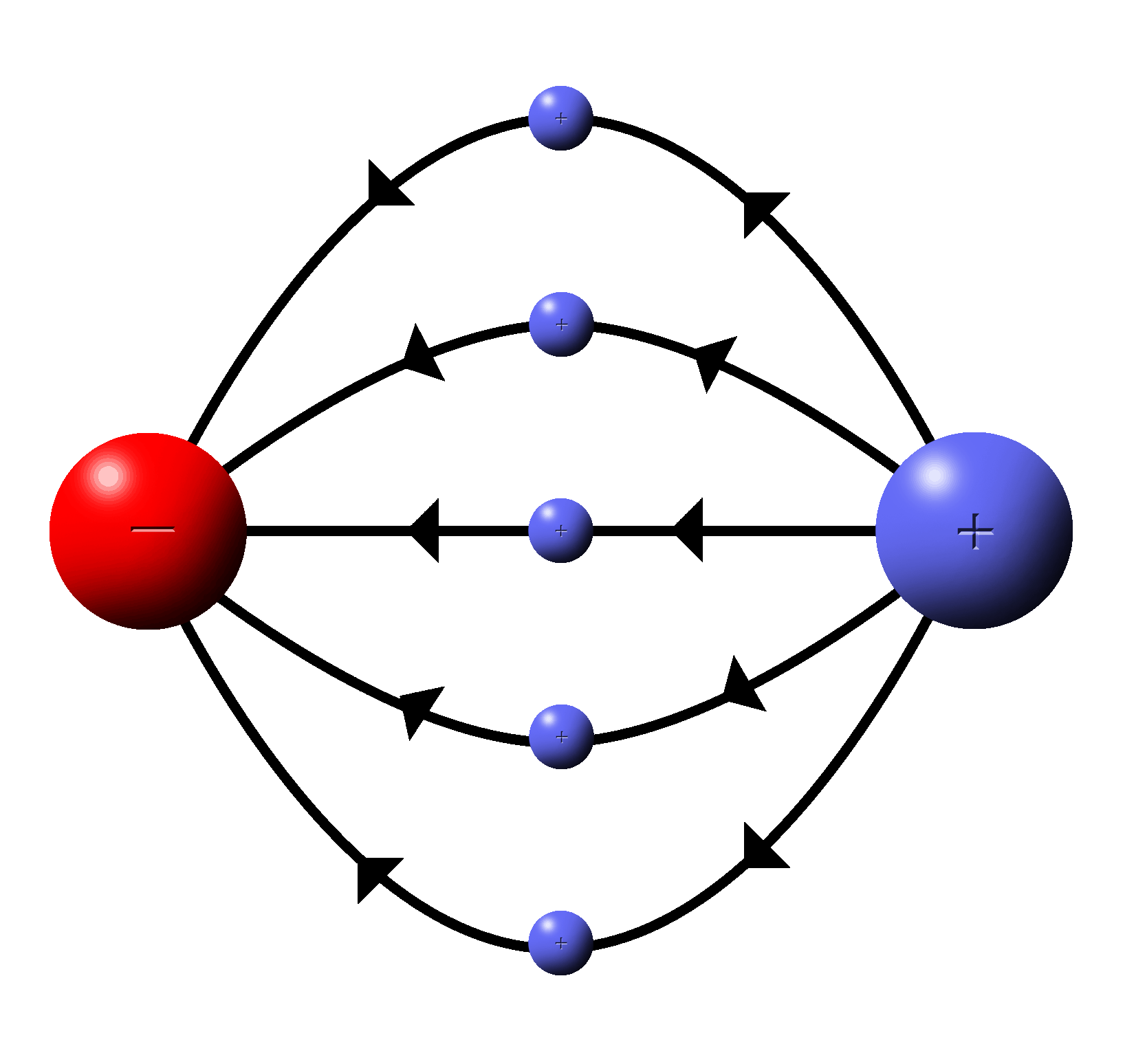 |
Since field lines are vector quantities the lines of flow gradually turn from one charge to the other rather than to go in straight lines. |
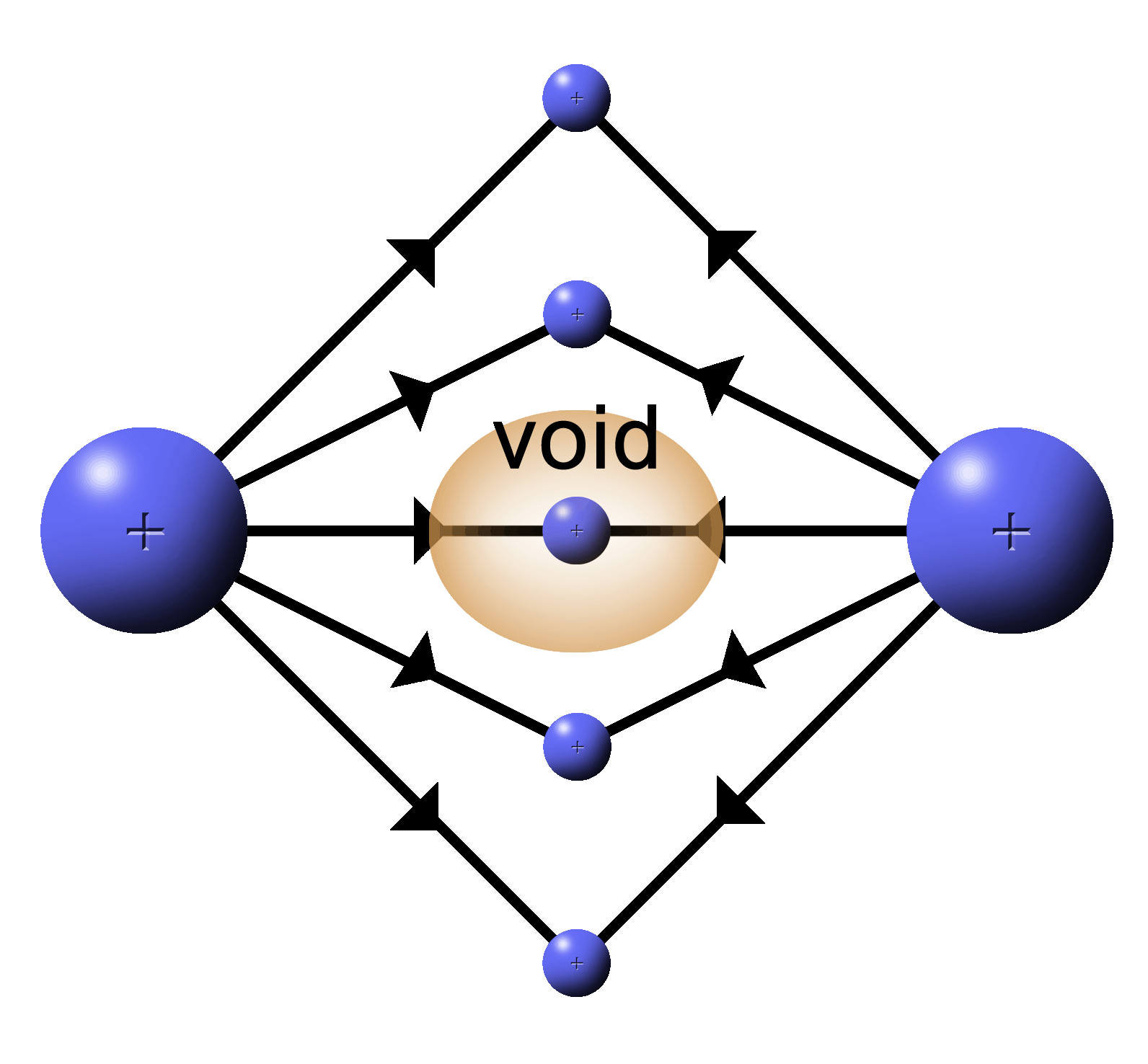 |
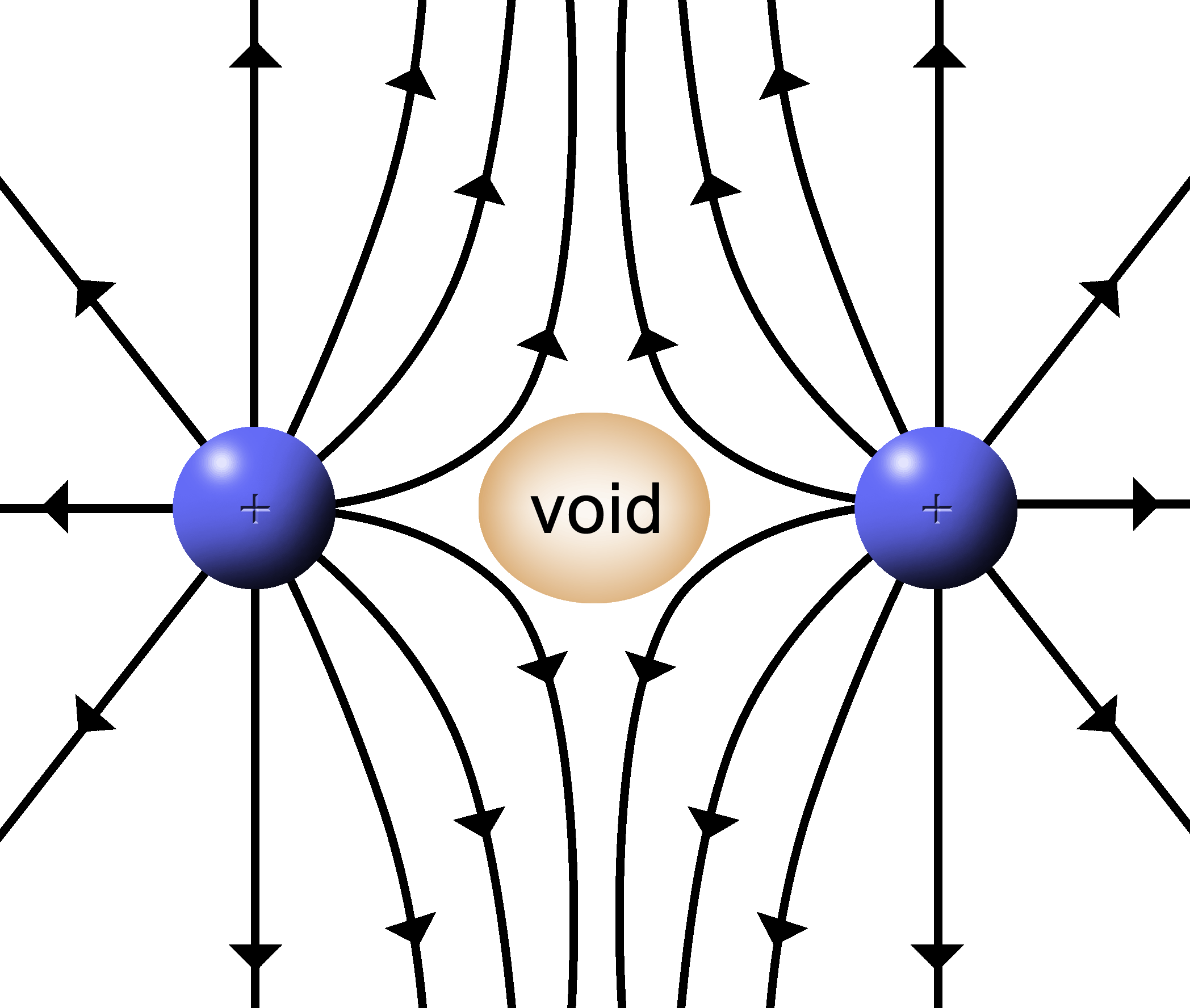
With two positive, push fields a couple of things happen:
1.
In the center where two lines meet head on, the field is cancelled by the opposing forces. A “void” is formed where the force of the E filed is zero. |
 |
2.
Where the lines hit at angles, the resultant field lines will be deflected. |
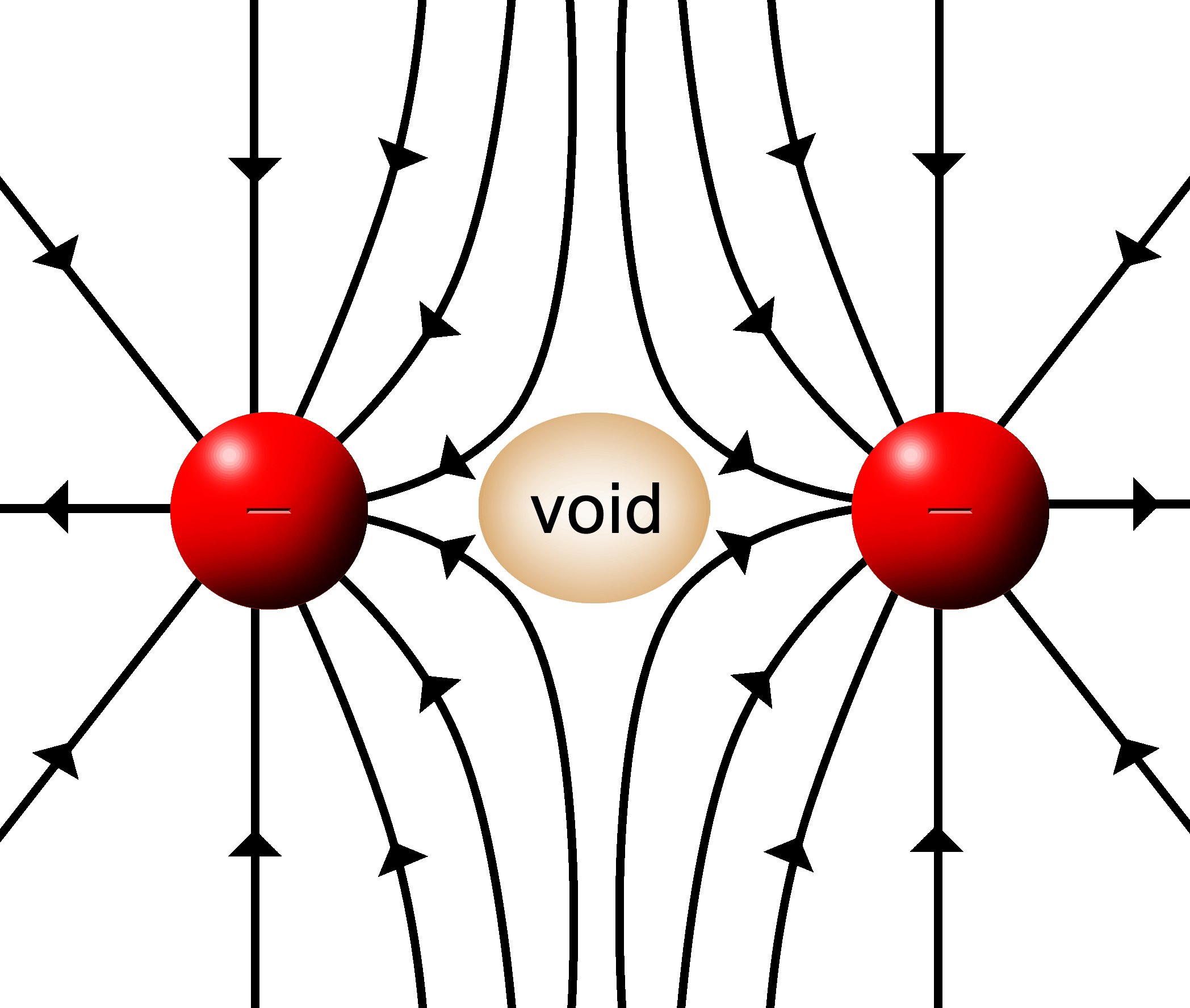 |
The same sort of thing will happen with two attractive fields.
|
Electric Fields Between Parallel Plates
|
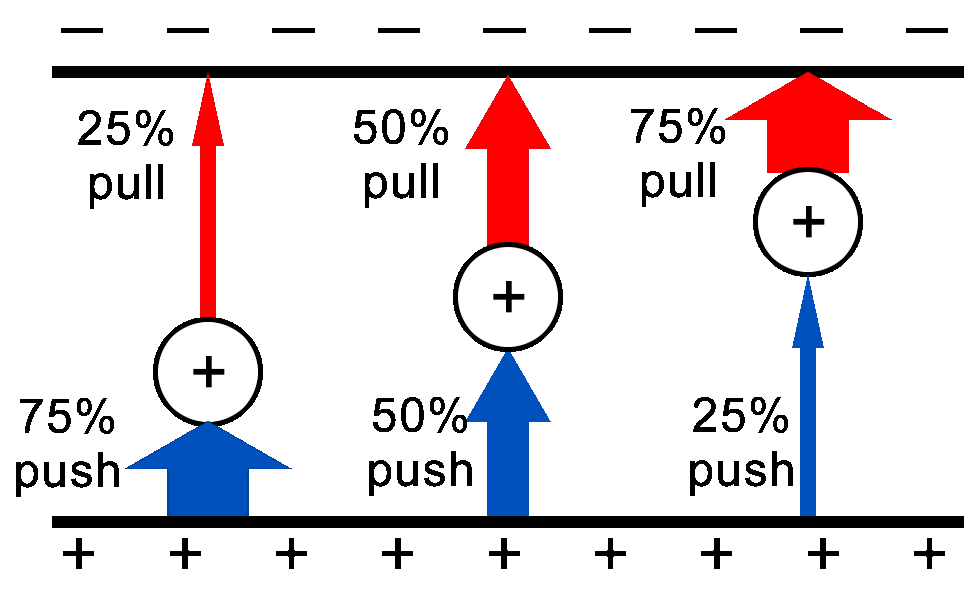
When a test charge is placed between two oppositely charged plates there will be a push force from the positive plate and a pull force from the negative plate. The force gets weaker as the charge gets further from the plate.
The left charge gets a very strong push (75% of the total forces) from the nearby positive plate and a weak pull (25%) from the faraway negative plate.
The middle charge which is halfway between the two plates gets half of the total force from the pushing positive plate and 50% of the force from the pulling negative plate.
The right charge gets 25% push from the positive and 75% pull from the negative.
|
|
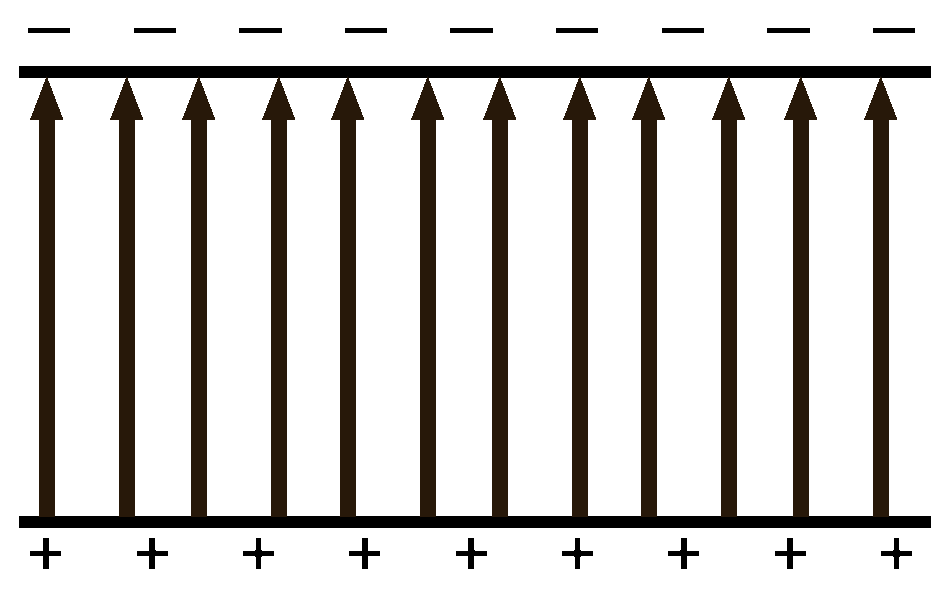
The net result is that no matter where you are between the plates, the test charge will get the same amount of force moving it towards the negative plate. It is a uniform field. |
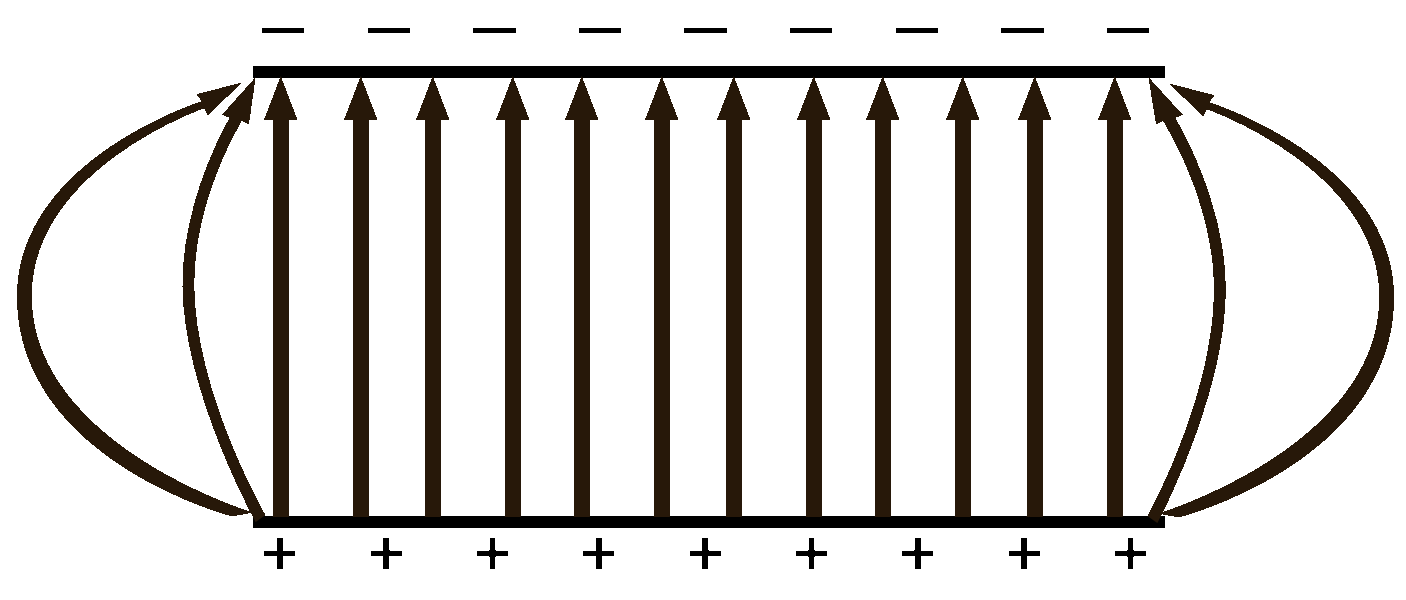 |
The uniformity breaks down at the edges. The edges start to act more and more like point charges and the field lines begin to curve from positive to negative. |
|
The field gets squished out like so much ice cream getting mooshed out from an ice cream sandwich. Which is an appropriate analogy because the two oppositely-charged plates are attracted towards each other just like the sandwich cookies are forced together as you bite down on it and the ice cream squirts out and dribbles down your cheeks and you have to wipe it off but when removing your fingers from the wafers it pulls off a layer of cookie that then clings to your fingertips like it was glue and when you wipe the ice cream off of your face you trade it with the chocolate cookie-glue which you are unaware of because it is not cold and wet like ice cream and you walk around with it on your face for the rest of the day along with the bits that stick to your teeth which also don’t notice and it looks like you are missing a tooth giving you an overall appearance of an olde English Dickens-era chimney sweep. But I digress! |
Milliken Oil Drop Experiment
Robert Millikan with some help from Harvey Fletcher set out to find the electrical charge of an oil drop. Through a clever series of conditions set up by the experimenters, he was able to find the value of an elementary charge.
Without getting into too much technical detail, here’s what he did:
|
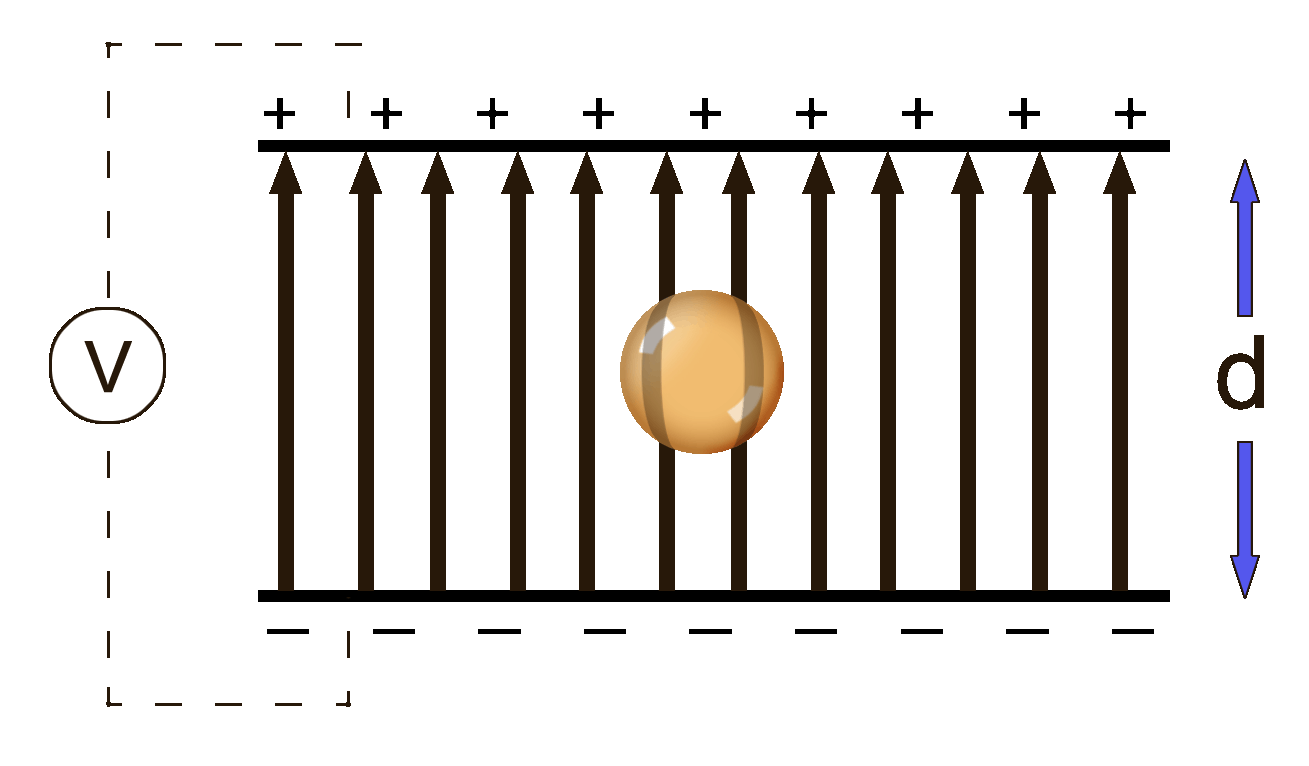 |
He shot oil through an atomizer which is a fancy spray bottle. The oil drops picked up a positive charge while coming through the nozzle something like rubbing a balloon on a sweater. The drops fell into a chamber that had two oppositely charged plates.
The droplets fell downward because of the force of gravity, of course. Milliken was able to adjust the voltage between the plates in such a way that the positive plate on the bottom was able to repel the positive oil droplet and counteract the force of gravity. Essentially, he was able to find the balance between downward gravity and the upward electric forces.
|
This relationship allowed him to measure the electric force. Since all the oil drops were of different sizes and masses, when he crunched all his data, there was one common factor in all his calculations and that was the value he discovered to be the charge of a single electron: the elementary charge: q = 1.6 x 10-19Coulombs. That’s where that comes from!
Follow the math below: |
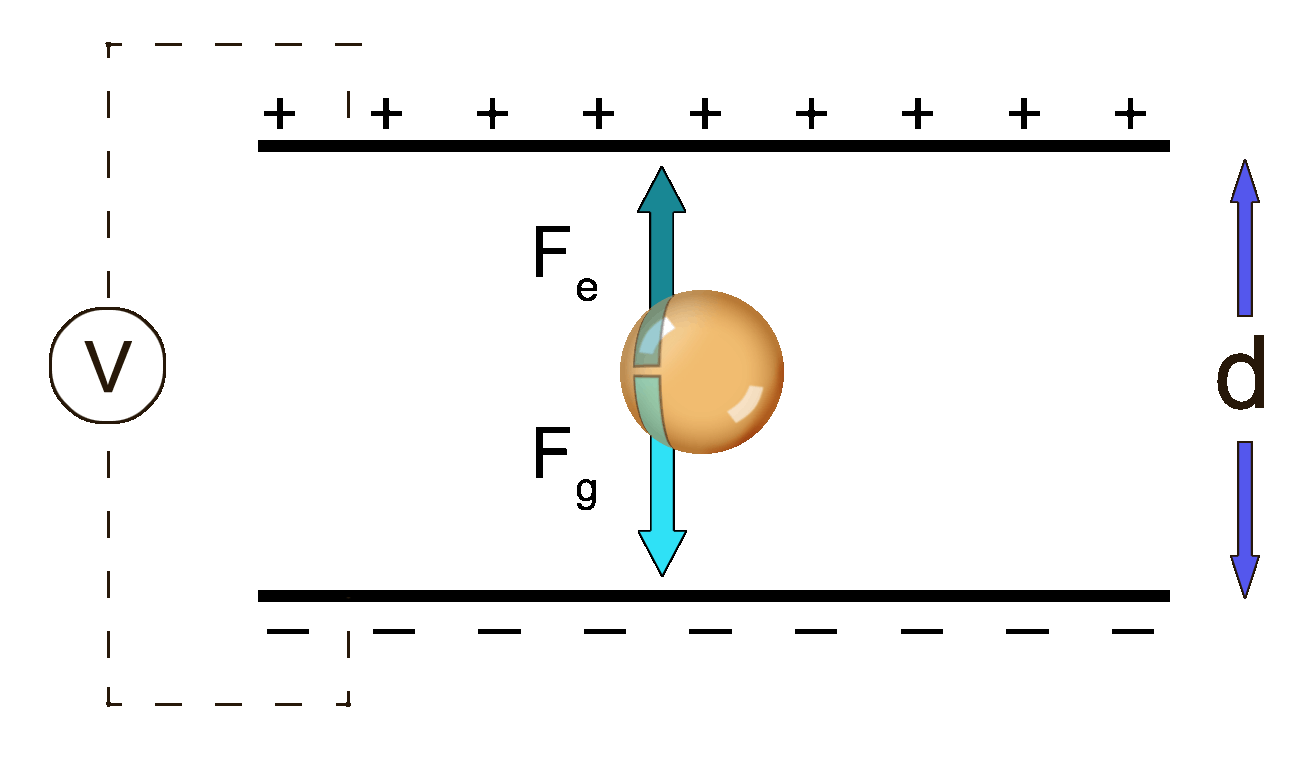 |
Fe = Fg
Fg = mg
So the equation now becomes: Fe = mg
Now a couple of step to get us ready to mess with Fe:
Voltage V = Work/q ∴
W = V•q
Also:
W = F•d (F is Fe in this case)
∴ Fe•d = V•q
Rearrange that into:
Fe/q = V/d
To solve for q:
q = Fe•d/V
Substitute mg for F:
q = mg•d/V |
-
Milliken knew the Voltage needed to suspend the oil drop.
-
He built the machine so he knew the distance between the plates.
-
He knew gravity (thanks Newton and Galileo!)
-
All that was left was the mass of the oil drop which changed for each drop.
-
He solved that problem with some clever thinking and insane math which I haven't gotten into here.
-
After calculating the charges for thousands of droplets he found one common value within his equations:
1.6 x 10-19Coulombs otherwise known as the charge for one single electron: 1e.
Ta-dah!
|
|